Starting with Archimedes with his principle of lift and the first mathematical description of gravity by Newton to Einstein’s theories of relativity and the research topics of our time based mostly on them, the subject of gravity offers a deep insight into physics. It can simultaneously take us into the depths of space and keep us on the surface of the earth with both feet on the ground.
This collection of questions about the physics of gravity is intended to give interested laymen basic insights into the fascinating subject of gravity.
For the more advanced reader there is corresponding literature recommended at the end of each article, which may include scientific publications from various journals (Nature, Science, Phys. Rev. Lett., etc.) depending on the topic.
Since this is a very broad and sometimes complicated subject area, we will add new information from time to time.
Metrology
Miscellaneous
When cooled to a very low temperature (below -139 °C or 134 K), superconductors conduct electric current without resistance, i.e. without losing energy. This property occurs due to the formation of so-called Cooper pairs. In this state, electrons can flow through the material of the superconductor without encountering resistance or obstacles. In high-temperature superconductors, unlike conventional ones, the superconductivity does not result from electron-phonon interaction and they are not metallic but ceramic materials [1], [2]. The name “high temperature superconductor” is based the fact that much higher transition temperatures can be achieved (Up to -23 °C or 250 K).
The history of superconductor research began in 1911, when Heike Kamerlingh Onnes was the first to succeed in cooling mercury down to about 4 K or – 269 °C using liquid helium (LHe), thus enabling research into metals in a previously unknown temperature range. At that time, ideas about how an electrical conduction mechanism might work in general were still very vague and incomplete [3], [4], [5].
During his experiments Onnes’s measuring instruments indicated that below the temperature of 4 K the metal (mercury) conducted the applied electric current without loss, the electrical resistance disappeared. In 1913, it was demonstrated that below a temperature of -266 °C also lead becomes superconducting, that its electrical resistance below that point disappears. In the following years, more and more materials were found that exhibited a similar behavior. If the temperature drops below the so called transition temperature, the respective material becomes a superconductor [3], [4], [5].
The idea of using superconductors for technical applications already existed in 1913. Since then physicists have been searching for other materials with a higher transition temperature, mainly to make the application more practical. The superconductor with the highest transition temperature (as far as currently known) is mercury cuprate becoming superconducting at 134 Kelvin ( -139 °C) and when pressurized at 153 K ( -120 °C). It is therefore considered a so-called high-temperature superconductor. Thanks to much higher transition temperatures, liquid nitrogen can be used instead of liquid helium, which makes the entire process much more economical and which is a great advantage of this kind of superconductor. However, these so-called cuprates are brittle and therefore difficult to process. There is also research in the field of material mixtures of e.g. iron, lanthanum, phosphorus, oxygen and arsenic, but so far only transition temperatures of 56 K ( -217 °C) could be achieved with them [4].
The question remains as to why superconductors behave the way they do. Basically, the concept of superconductivity is based on the occurrence of a macroscopic, coherent matter wave causing the formation of Cooper-pairs (electron pairs). Established in 1957 by John Bardeen, Leon Cooper and Robert Schrieffer this theory is now known as BCS theory. It states that electrons in a superconductor are coupled into pairs due to interactions between electrons and the crystal lattice at low temperatures. The behavior of high temperature superconductors is only partially described by the theory and not fully understood down to the present day.[6], [7].
One of the latest discoveries in 2018 were ultrathin layers of carbon also exhibiting superconducting properties. When two graphene layers are superimposed and twisted against each other by an angle of 1.3 degrees, superconducting properties are exhibited when cooled down to a temperature of 1.65 K (-271.5 °C). Scientists hope to be able to study the behavior of the so-called unconventional superconductors (high-temperature superconductors) with the twisted graphene layers in more detail [8], [9].
[1] Spektrum: Supraleiter, (Link: https://www.spektrum.de/thema/supraleiter/1314677), accessed 06 May 2020 [2] Welt der Physik: Supraleiter, (Link: https://www.weltderphysik.de/gebiet/materie/supraleiter/), accessed 06 May 2020 [3] Buckel, Werner; Kleiner, Reinhold: Supraleitung – Grundlagen und Anwendungen; WILEY-VCH; 2004 [4] Pollmann, Maike: Welt der Physik: Geschichte der Supraleitung, (Link: https://www.weltderphysik.de/gebiet/materie/supraleiter/geschichte/), 07.04.2011; accessed 07 May 2020 0 [5] Onnes, Heike Kamerlingh; Edited by Gavroglu, Kostas; Goudaroulis, Yorgos: Through Measurement to Knowledge: The Selected Papers of Heike Kamerlingh Onnes 1853- 1926; Boston Studies in the Philosophy of Science Volume 124; 1991[6] Tipler, Paul; Llewellyn, Ralph: Moderne Physik; Oldenbourg; 2010
[7] Cooper, Leon N.; Feldman, Dmitri: BCS: 50 Years; World Scientific Publishing CO. Ptc. Ltd.; 2011 [8] Löfken, Jan Oliver: Welt der Physik: Supraleiter aus Kohlenstoff, (Link: https://www.weltderphysik.de/gebiet/materie/news/2018/supraleiter-aus-kohlenstoff/), 05.03.2018, accessed 07 May 2020 [9] Cao, Yuan; Fatemi, Valla; Fang, Shiang; et. Al.: Unconventional superconductivity in magic-angle graphene superlattices; Nature 556; 05.03.2018Further reading:
[10] Kempf, Achim: Could the Casimir Effect explain the Energetics of High-Temperature Superconductors?; arXiv 03/2006 [11] Kiehn, R. M.: Are There Three Kinds Of Superconductivity?; International Journal of Modern Physics B, 06/1991 [12] Rao, C. N. R.; Raychaudhuri, A. K.: CRC Handbook of chemistry and physics, CRC Press, 2004 [13] Donglu, Shi: High-Temperature Superconducting Materials Science and Engineering: New Concepts and Technology, Pergamon Press, 1995 [14] Mankowsky, Roman: Supraleitung bei Raumtemperatur; Physik in unserer Zeit Colume 46, 09/2015More about gravity
Gravity is the property of masses to attract each other. The force of attraction depends on the size of the masses and their distance. It decreases quadratically with distance. The first one to experimentally proof mass attraction with a torsion balance in 1798 was Cavendish.
The size of the earth’s gravitional pull or gravity acceleration g depends on the mass distribution in the earth.
The size of the earth’s gravitational pull or gravity acceleration g depends on the mass distribution in the earth. The more masses are below one up to the centre of the earth or the higher the density of this mass, the higher the gravitational pull. The local acceleration due to gravity can be measured with a gravimeter. From this, conclusions can also be drawn about the nature of the subsurface, e.g. cavities or ore deposits.
Gravitational acceleration depends on latitude and height above sea level. At sea level, at the equator g=9.780 m/s2, at the 45th parallel g=9.807 m/s2 and at the pole g=9.832 m/s2. With every additional height meter g decreases by about 3*10 -6 m/s2, as long as h is small against the earth radius.
At the equator the distance from the centre of the earth is greater and thus the gravity acceleration is lower than at the poles.
In addition, the centrifugal force counteracts the gravitational acceleration due to the earth’s rotation, so that this is lower at the equator. The effect is about 3 Gal.
The local absolute values of the acceleration due to gravity can be obtained from the Land Surveying Offices.
Tides are created by the rotation of the Earth and Moon around the common centre of mass. The difference forces between gravitational and centrifugal forces are decisive. These forces ensure that a flood mountain is formed on the Earth both on the side facing the Moon and on the side facing away from the Moon. Therefore, there are ebb and flow twice a day. In addition, the sun also exerts an influence on the tides, which results in spring tides by addition at new and full moon and nipp tides by subtraction at half moon.
The tidal forces can be measured with a gravimeter at any place on earth, independent of the tidal range of the oceans. They are in the range of 0.5 mGal to 1.1 mGal.
“Capital G” is the constant of proportionality in Newton’s law of gravit. It established a formal relationship between the masses, the distance and the resulting gravitational force. It is now assumed that G is not constant, but could depend on other, previously unknown factors.
Recognized CODATA value of 2010:
G = (6,67348 +/- 0,00080) 10 – 11 m³ kg-1 s-2. The accuracy of this value is only 0.15 %, which is very inaccurate for a fundamental constant.
“Small g” refers to the acceleration with which a freely falling body increases its velocity in the Earth’s gravitational field. Average value: G = 9.80665 m/s² (CODATA value of 2010).
‘Gal’ stands for Galileo and is another unit for the acceleration of gravity g, which is mainly used in geophysics. It is 1 Gal = 10 -2 m/s², thus g= 981 Gal. For the description of small effects mGal = 0.001 Gal is mostly used.
On earth, artificial weightlessness can only be achieved by letting a body fall freely. This is achieved in parabolic flights with airplanes or in drop towers. The achievable duration ranges from a few seconds (drop tower) to a few minutes (parabolic flight).
Places like Roca di Papa in Italy or Karpacz Gorny in Poland are known for so-called “gravitational anomalies”. Only precise measurements could clarify what these phenomena are really about. The most obvious explanation is an optical illusion that makes you think that things are going uphill, although in reality they are going downhill. The fact that a nearby mountain changes the direction of gravity is practically impossible due to the much too small mass in relation to the earth.
Theory of relativity
The General Theory of Relativity was established by Albert Einstein in 1915, at that time without any empirical basis.
In the following years several experiments were performed to confirm the different predictions of GR. In general, the experiments can be divided into classical and modern ones. One of the classical experiments is about the perihelion rotation of the planet Mercury. Already at the end of the nineteenth century astronomers noticed a discrepancy of 43″ arc seconds in one hundred years between the measurements of the speed of the perihelion rotation and the predictions of the Newtonian theory used at that time. In 1916, only a few years later, Einstein was able to calculate the discrepancy exactly and thus explain it with his General Theory of Relativity, which had been established shortly before. Again three years later the theory had its public breakthrough when astronomer Arthur Eddington in 1919 could show in his experiments that the light of a star is deflected by the gravitational field of the sun and thus space is curved according to Einstein’s theory [6]. Applying Newton’s theory, a curvature of space could be calculated as well, but it would yield a different result than GR. Eddington’s experiment was performed during a solar eclipse, because only then starlight can be observed simultaneously with the eclipsed sun. The setup is shown in the following figure.
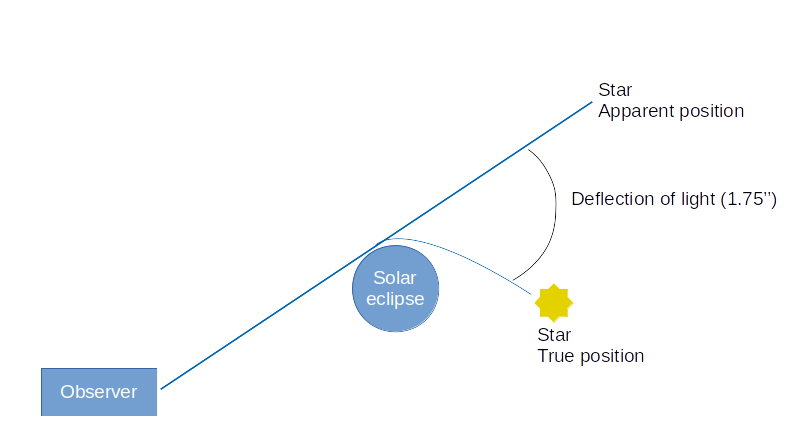
Light from a star passing close to the Sun can be observed on Earth when deflected by the Sun’s own gravitational field. Actually, the star itself is not visible as its true position (from the observer’s point of view) is behind the Sun. However, the true position of the star can be calculated and is found to be 1.75 arcseconds using GR. In Eddington’s experiment this result of GR could be confirmed with an uncertainty of 20%. Since the first measurement in 1919, the experiment has been repeated and confirmed many times with a higher accuracy [1] [2] [3].
Another result of general relativity was the gravitational redshift, i.e. the change of the light frequency into the red (smaller wavelengths) when light moves from a larger to a smaller gravitational potential. This frequency change can also be calculated with GR. In an experiment of the physicists Pound and Rebka in 1960 the described frequency change could be demonstrated [7]. The setup was in a tower, with a light source with gamma radiation at the bottom (the earth potential) and radiating about 22.6 m vertically upward to the top of the tower (tower potential). Simplified the change of the frequency can be described by
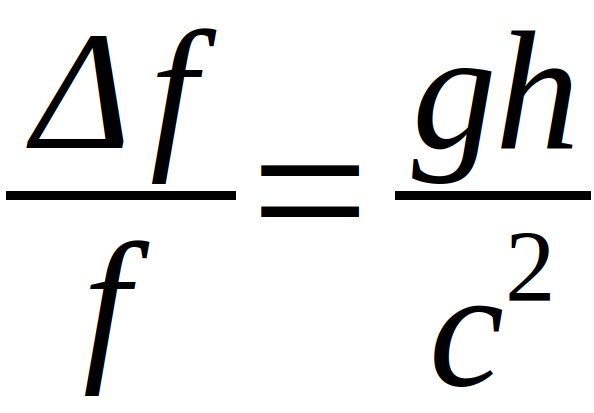
With g being the gravitational acceleration, h the height of the tower and c the speed of light. The uncertainty measured in the experiment corresponded to the theoretical prediction
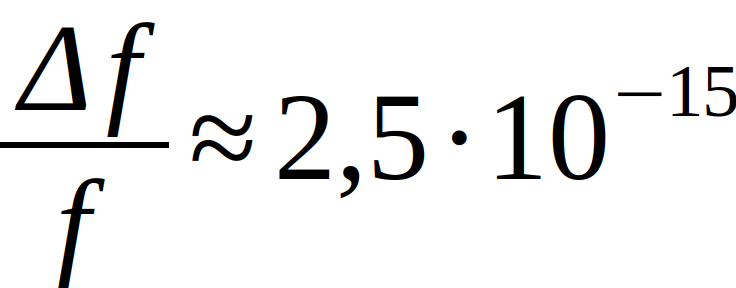
of about 1 %. By means of the so-called Mößbauer effect it was possible to measure such a small deviation of the frequencies. A red shift is also caused by the expansion of space [1] [4].
Shapiro performed another experiment in 1968 and 1971: a radar transit time measurement. Venus, sun and earth lie on a straight line with the distances r1 from the earth to the sun and the distance r2 from Venus to the sun, whereby the Venus, seen from the earth, lies behind the sun [9] [10] [11].
A radar signal is now sent from Earth to Venus, reflected there and then registered again on Earth. According to a prediction of GR also the transit time of light is changed when it comes near a large mass. Using Newtonian physics, the transit time can be calculated as follows
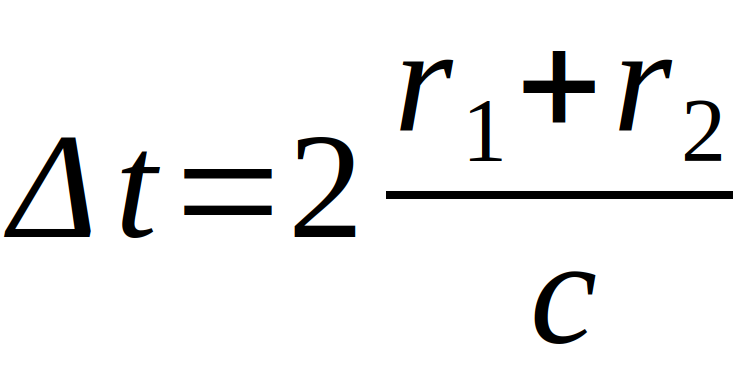
Basing on Einstein’s equations following deviation (simplified expression) can be calculated:
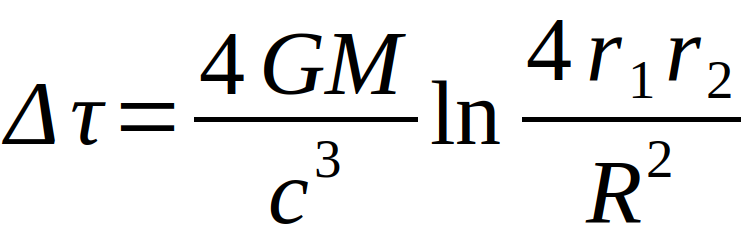
Where G is Newton’s gravitational constant, M is the mass of the sun, R is the radius of the sun, and c is the speed of light. In Shapiro’s experiments, the calculated deviation was very well demonstrated experimentally [1].
In 1971, Hafele and Keating performed an experiment comparing the time displayed on a clock on Earth to that on a clock positioned in an airplane [12]. For an equatorial trajectory, according to the general theory of relativity, the following results are obtained
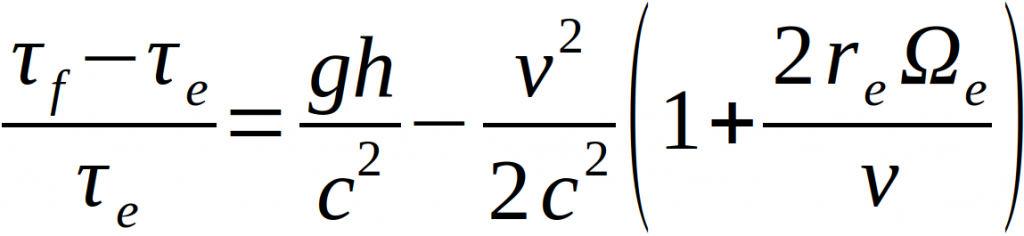
With τf and τe being the proper times for the flight orbit in the airplane or on the earth, g the gravitational acceleration, h the height of the airplane, real earth radius, e the rotational speed of the earth and c the speed of light. The first term is derived from GR to include gravity, the second term is deduced from special relativity. Theoretically, this results in
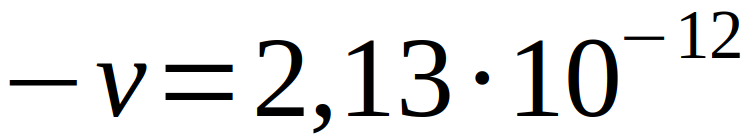
and
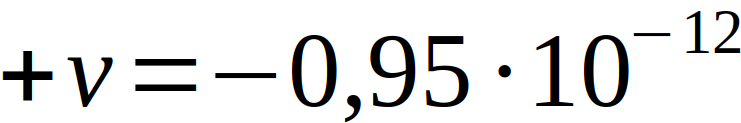
which could be measured with the atomic clocks used.
A further, well-known experiment is the Gravity Probe B experiment that was able to prove the Geodesic Effect and the Lense Thirring Effect.
In addition, the equations of GR contain so-called gravitational waves. Like electromagnetic waves these waves propagate at the speed of light, being generated whenever masses are accelerated, e.g. moving planets. The waves’ intensity is extremely low and additional to that they are affected by many external disturbances. Therefore detection of gravitational waves is a very difficult task. In the 1960s, the physicist Joseph Weber tried to measure the expansion of an aluminum cylinder caused by gravitational waves, but without success [8] [13].
[1] Sonne, Bernd: Allgemeine Relativitätstheorie für jedermann: Grundlagen, Experimente und Anwendungen verständlich formuliert; Springer Spektrum; 2. Auflage; 2018 [2] Welt der Physik: Albert Einstein und die Relativitätstheorie; (Link: https://www.weltderphysik.de/thema/albert-einstein-und-die-relativitaetstheorie/), accessed 19 November 2020 [3] Fließbach, Thorsten: Allgemeine Relativitätstheorie; Springer Spektrum; 7. Auflage; 2016 [4] Göbel, Holger: Gravitation und Relativität: eine Einführung in die Allgemeine Relativitätstheorie; De Gruyter Studium; 2014 [5] Einstein, Albert: Die Grundlage der allgemeinen Relativitätstheorie; 1923 [6] Eddington, Sir Arthur: Space, Time and Gravitation – An Outline of the General Relativity Theory; Cambridge University Press; 1920 [7] Pound, R. V.; Rebka, G. A. Jr.: Gravitational Red-Shift in Nuclear Resonance; The Physical Review Journals Celebrate The International Year of Light; Phys. Rev. Lett. 3, 439; 01.11.1959 [8] Weber, J.: Gravitational Radiation; Phys. Rev. Lett. 18, 498; 27.03.1967 [9] Ash, M. E.; Campbell, D. B.; Dyce, R. B.; Ingalls, R. P.; Jurgens, R.; Pettengill, G. H.; Shapiro, I. I.: The Case for the Radar Radius of Venus; Science Vol 160, Issue 3831, 31.05.1968 [10] Shapiro, Irwin I.: Radar Observations of the Planets; Scientific American Vol. 219, No. 1; 07/1968 [11] Shapiro, Irwin I.; Ash, Michael E.; Ingalls, Richard P.; Smith, William B.; Campbell, Donald B.; Dyce, Raymond F. Jurgens; Pettengill, Gordon H.: Fourth Test of General Relativity: New Radar Result; Phys. Rev. Lett. 26; 1132; 03.05.1971 [12] Hafele, J. C.; Keating, Richard E.: Around-the-World Atomic Clocks: Predicted Relativistic Time Gains; Science Vol 177, Issue 4044; 14.07.1972 [13] Everitt, C. W. F. et al.: Gravity Probe B: Final Results of a Space Experiment to Test General Relativity; Phys. Rev. Lett. 106, 221101; 31.05.2011Further reading:
[14] Eddington, Sir Arthur: Report on the relativity theory of gravitation; Minkowski Institute Press; 2014 [15] Horst, Wegener: Der Mössbauer-Effekt und seine Anwendungen in Physik und Chemie; Bibliographisches Institut, Mannheim; 1965 [16] Shapiro, Irwin I.; Pettengill, Gordon H.; Ash, Michael E.; Stone, Melvin L.; Smith, William B.; Ingalls, Richard P.; Brockelman, Richard A.: Fourth Test of General Relativity: Preliminary Results; Phys. Rev. Lett. 20, 1265; 27.05.1968, Erratum Phys. Rev. Lett. 21, 266; 1968 [17] Shapiro, Irwin I.: Planetary radar astronomy; IEEE Spectrum Volume 5, Issue 3; 05/1968 [18] Rodrigues Jr., W. A.; de Oliveira, E. C.: A comment on the twin paradox and the Hafele-Keating experiment; Physics Letters A; Volume 140, Issue 9; 16.10.1989 [19] Schlegel, Richard: Comments on the Hafele-Keating Experiment; American Journal of Physics 42, 183; 1974 [20] Everitt, C. W. F.; Mulfelder, B.; DeBra, D. B.; Parkinson, B. W.; Turneaure, J. P.; Silbergleit, A. S.; Acworth, E. B.; Adams, M.; Adler, R.; Bencze, W. J.: The Gravity Probe B test of general relativity; Classical and Quantum Gravity, Volume 32, Number 22; 17.11.2015 [21] Buchman, Saps; Everitt, C. W. F.; Perkinson, B.; et. Al.: The Gravity Probe B Relativity Mission; Advances in Space Research; Volume 25, Issue 6, 2000 [22] Conklin, John W.; Gravity Probe B Collaboration: The Gravity Probe B experiment and early results; Journal of Physics: Conference Series, Volume 140, Issue 1; 2008Zero-point energy
The Casimir effect was first calculated and predicted by physicist Hendrik Brugt Gerhard Casimir in 1948. The experimental proof followed in 1956. The effect states that two parallel metal plates (or conductive plates) attract each other in vacuum, respectively that a force, the Casimir force, acts on them, pressing the plates together [1] [2] [3] [4] [5].
To explain the Casimir effect, a short explanation what vacuum is made of is necessary. Vacuum is defined as a quantum field, i.e. as a superposition of different field configurations with large and small wavelengths. According to quantum field theory every vacuum contains energy, the so-called zero point energy (ZPE) or vacuum energy. This kind of energy however can not be extracted, because the vacuum itself is already the lowest energy state. Although the quantum vacuum seems to consist of “nothing”, it is actually a very complex structure, making it impossible to completely deplete a space of all particles. Particles in this apparently empty space always exist only for a short time, leading to fluctuations in the quantum vacuum [2], [3].
The Casimir effect is based on the fact that an electric field on parallel metal plates can only be perpendicular. This severely limits how these fields can form in the region between the plates. Configurations with wavelengths longer than the plate spacing are no longer possible. In this region the vacuum is in a different state than in the “undisturbed” vacuum. Due to such a restriction of possibilities, the zero-point energy decreases there. If the plates are now pushed even closer together, this effect is further intensified, the plates attract each other and a small but measurable energy is gained [1], [2].
In recent years the Casimir effect has become more important and more relevant again. By means of modern measurement techniques such as atomic force microscopy, it is possible now to measure smaller and smaller forces with much higher accuracy. There is also an increased interest from a technological point of view, as the Casimir force becomes particularly important for miniature machines in the micro- and nanometer range. In fundamental research and especially with respect to the effort to unify gravity (i.e. theory of relativity) and quantum mechanics, the Casimir force also plays an important role in experimentally proving the fundamental forces assumed by physicists. Since these forces change Newton’s law of gravity for distances in the submillimeter range, it is important to be able to predict and calculate the Casimir force [6].
[1] Spektrum: Lexikon der Astronomie: Casimir-Effekt; (Link: https://www.spektrum.de/lexikon/astronomie/casimir-effekt/61), accessed 14 May 2020 [2] Physik Cosmos indirekt; (Link: https://physik.cosmos-indirekt.de/Physik-Schule/Casimir-Effekt), accessed 14 May 2020 [3] Spektrum: Lexikon der Astronomie: Quantenvakuum; (Link: https://www.spektrum.de/lexikon/astronomie/quantenvakuum/376), accessed 18 May 2020 [4] Plunien, Günter; Müller, Berndt; Greiner, Walter: The Casimir effect; Physics Reports Volume 134; 03/1986 [5] Casimir, H. B. G.: Mathematics. – On the attraction between two perfectly conducting plates; Gems from a century of science 1898-1997; 29.05.1948 [6] Lambrecht, Astrid: Das Vakuum kommt zu Kräften; Physik Unserer Zeit, 2005Further reading:
[7] Milton, Kimball A.: The Casimir Effect: Physical Manifestations of Zero-Point Energy; University of Oklahhoma, 02/2008 [8] Antonini, P.; Bimonte, G.; et. Al.: An experimental apparatus for measuring the Casimir effect at large distances; 12/2008 [9] Quach, James Q.: Gravitational Casimir effect, 02/2015 [10] Mostepanenko, V. M.: Experiment, theory and the Casimir effect, 03/2009 [11] Bachmann, Sven; Kempf, Achim: The Transplanckian Question and the Casimir Effect, 04/2005 [12] Bordag, M.; Mohideen, U.; Mostepanenko, V. M.: New developments in the Casimir effect; Physics Reports Volume 353; 10/2001