Laut der Theorie der Dunklen Materie soll diese circa 27 % der gesamten Energiedichte des Weltalls ausmachen. Diese Theorie wurde Anfang des 20. Jahrhunderts aufgestellt, als Wissenschaftler bei Untersuchungen von Bewegungen von Galaxien im Coma-Galaxienhaufen feststellten, dass die leuchtende Materie, z.B. von Sternen, Gas und Staub, nicht ausreicht, um das Rotationsverhalten erklären zu können [1] [2] [3].

Grundsätzlich existieren sechs verschiedene Theorien zur Natur der Dunklen Materie. Eine dieser ist die der Versteckten gewöhnlichen Materie. Im Rahmen dieser Theorie gingen Astronomen davon aus, dass noch nicht sämtliche gewöhnliche Materie entdeckt wurde und schrieben die fehlende Masse kalten Gas- oder Staubwolken, erkalteten Braunen Zwergen und ähnlich massereichen Körpern (MACHOs: „Massive Astrophysical Compact Halo Objects“) oder gar Schwarzen Löchern zu [2].

Eine sehr beliebte und verbreitete Theorie ist die der sogenannten WIMP-Teilchen. Diese sind schwere Teilchen der sogenannten WIMP-Klasse (weakly interacting heavy particles), welche kaum oder gar nicht elektromagnetisch strahlen und außerdem nur eine schwache Wechselwirkung besitzen. Bis heute konnte keines der Teilchen nachgewiesen oder experimentell in einem Teilchenbeschleuniger hergestellt werden, es werden jedoch verschiedene Ansätze verfolgt [2], [4], [5].

Die Experimente, die durchgeführt werden, um Dunkle Materie in Form von WIMPs nachzuweisen, lassen sich in drei Gruppen einteilen: Experimente in der Luft bzw. im Weltall, Untergrundexperimente und Beschleunigerexperimente. Bei den Versuchen in der Luft bzw. dem All existiert die Annahme, dass sich zwei WIMPs beim Aufeinandertreffen auslöschen und Energie in Form eines Photons freisetzen. Um diese bzw. ihre Folgeprodukte (Elektronen und Positronen) nachzuweisen bevor sie mit Luftmolekülen reagieren, werden die Experimente bevorzugt im Weltall durchgeführt [3], [6], [7].

Im Rahmen der Untergrundexperimente soll die Wechselwirkung eines WIMPs mit gewöhnlicher Materie in einem speziellen Detektor nachgewiesen werden. Um den Detektor bestmöglich gegen störende kosmische Strahlung und Störquellen abzuschirmen, werden die Versuche in Laboren in ehemaligen Minen oder unter Bergen durchgeführt. Das Problem ist, dass die gesuchten Wechselwirkungen extrem selten sind und deswegen sowohl viel Material als auch lange Messzeiten erforderlich sind [3], [8].

Die Idee der Beschleunigerexperimente ist die künstliche, mit hohem Energieaufwand verbundene Erzeugung Dunkler Materie. Außerdem sind anspruchsvolle Algorithmen notwendig, die diejenigen Prozesse, in denen WIMPs entstehen können, aus den vielen Ereignissen herauszufiltern. Bemerkbar könnte beispielsweise fehlende Energie sein, da WIMPs unsichtbar sind, aber viel kinetische Energie mitsichtragen [3].

Axionen, Teilchen, die milliardenfach leichter als Elektronen sind, beschreiben einen weiteren Ansatz für die Natur der Dunklen Materie. Es könnte sich hierbei um einen einzelnen Elementarteilchen-Typen oder gar um eine ganze Gruppe unbekannter Teilchen handeln. Detektoren zum Aufspüren dieser Axione haben bislang keinen Hinweis auf ihre Existenz erbracht [2].

Die Theorie der Heißen Dunkle Materie beschreibt diese als bestehend aus Teilchen, die extrem schnell unterwegs und neutrinoähnlich sind. Dunkle Materie scheint generell wie Gaswolken zu konzentrieren, da heiße Dunkle Materie jedoch auseinanderstreben würde, könnte sie nur einen kleinen Teil der gesamten Dunklen Materie ausmachen [2], [9], [10].

Ein weiterer Ansatz ist der der sterilen Neutrinos. Diese Theorie beschreibt eine Mischung der zuvor vorgestellten Ansätze hypothetischer Teilchen. Die Masse dieser variiert jedoch je nach Modell und auch mögliche Wechselwirkungen unterliegen verschiedener Theorien. Das MiniBooNE-Experiment am Fermilab bei Chicago versucht solche Teilchen zu finden [2], [11].

Die zuvor vorgestellten Ansätze bestanden durchweg aus hypothetischen Teilchen. Ein gegensätzlicher Ansatz ist der modifizierter Gravitationstheorien. Die Idee ist, dass die Gesetze der Schwerkraft in den Weiten der Alls nicht in der Form gelten, wie auf der Erde – Somit würden die Messdaten, die man durch die Existenz Dunkler Materie versucht zu erklären, plötzlich Sinn ergeben [2], [12], [13], [14].

Bisher konnten keine Teilchen nachgewiesen werden und keiner der Ansätze experimentell bestätigt werden, die Forschung um die Dunkle Materie wird also vermutlich noch einige Jahre oder Jahrzehnte andauern, bis Antworten gefunden werden.

[1] Spektrum Lexikon der Astronomie: Dunkle Energie, (Link: https://www.spektrum.de/lexikon/astronomie/dunkle-energie/83), aufgerufen am 09.07.2020

[2] Eidemüller, Dirk: Sechs Erklärungen für die Dunkle Materie, (Link: https://www.spektrum.de/news/sechs-erklaerungen-fuer-die-dunkle-materie/1719160), aufgerufen am 09.07.2020

[3] Welt der Physik: Dunkle Materie, (Link: https://www.weltderphysik.de/gebiet/universum/dunkle-materie/), aufgerufen am 09.07.2020

[4] Burkert, Anderas; Silk, Joseph: Dark Baryons and Rotation Curves, 16.09.1997, The American Astronomical Society; The Astrophysical Journal Letters, Volume 488, Number 2

[5] Barna, I. F.: Searching for dark matter with helium atom

[6] Pospelov, Maxim; Ritz, Adam; Voloshin, Mikhail: Secluded WIMP dark matter, 10.04.2008, Physics Letter B

[7] Liu, Jianglai; Chen, Xun; Ji, Xiangdong: Current status of direct dark matter detection experiments, 02.03.2017

[8] Jochum, Josef; von Feilitzsch, Franz: Dunkle Materie und Sonnen-Neutrinos: Eine endliche Neutrinomasse weist auf bisher unbekannte Teilchen jenseits des Standardmodells hin, 20.02.2013, Physikalische Blätter, Volume 56, Issue 3

[9] Gribbin, John; Rees, Martin: Zwei Arten dunkler Materie, Ein Universum nach Maß, 1989

[10] Grupen, Claus: Dunkle Energie und Dunkle Materie, Einstieg in die Astroteilchenphysik, 31.10.2017

[11] Dodelson, Scott; Widrow, Lawrence M.: Sterile neutrinos as dark matter, Phys. Rev. Lett. 72; 03.01.1994

[12] Aguilar-Arevalo, A.A.; Anderson, C.E.; et. Al.: Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment: The MiniBooNE detector, 01.02.2009

[13] BooNE: Booster Neutrino Experiment, (Link: https://www-boone.fnal.gov/index.html), aufgerufen am 26.08.2020

[14] Bekenstein, Jacob D.: Modified gravity as an alternative to dark matter

Weiterführende Literatur:

[15] Kroupa, P.; Famaey, B.; et. Al.: Local-Group tests of dark-matter concordance cosmology: Towards a new paradigm for structure formation

[16] Kroupa, Pavel; Pawlowski, Marcel: Das kosmologische Standardmodell auf dem Prüfstand (Spektrum der Wissenschaft, August 2010)

[17] Van Dokkum, Pieter; Danieli, Shany; et. Al.: A galaxy lacking dark matter

Die Dunkle Energie beschreibt eine hypothetische Energieform, welche bei Betrachtung der Massenverteilung im Universum circa 68 % der Gesamtmasse ausmacht. Sie beschreibt ein Energiefeld, welches den Kosmos beschleunigt und auseinandertreibt und der Schwerkraft im Weltall entgegenwirkt, also die Expansion bremst. Das bedeutet, nach heutiger Erkenntnis, dass sich das Universum immer weiter ausdehnen wird. Während Physiker für die Natur der Dunklen Materie konkrete Lösungsansätze haben, ist es bei der Dunklen Energie erheblich schwieriger [1] [2].

Eingeführt bzw. erfunden wurde der Begriff der Dunklen Energie 1998 von dem Kosmologen Michael S. Turner. Nach seiner Definition meint diese Bezeichnung eine Energieform, die weder baryonische noch Dunkle Materie ist. Da diese Energie sich nicht durch elektromagnetische Strahlung bemerkbar macht, wird sie „dunkel“ genannt. Ursprünglich eingeführt wurde sie als eine Verallgemeinerung der kosmologischen Konstante, um die zu beobachtende Expansion des Universums erklären zu können. Nachdem diese Expansion durch die Rotverschiebung der Galaxien generell als etabliert galt, wurden unterschiedlichste Messungen durchgeführt, um zum einen die Geschwindigkeit der Expansion und zum anderen ihre Veränderung mit der Zeit zu bestimmen. Diese Messungen der Entfernung weit entfernter Supernovae vom Typ Ia ergaben, entgegen der bis dahin gültigen Annahmen, eine Zunahme der Expansionsgeschwindigkeit. Dieses Phänomen wurde auf die Dunkle Energie zurückgeführt [2] [3] [4] [5].

Es gibt eine Vielzahl verschiedener Ansätze für die physikalische Erklärung der Natur der Dunklen Energie. So wird sie häufig als die sogenannte Vakuumenergie interpretiert, in anderen Modellen als zeitabhängige Größe oder als Naturkonstante, welche eine Raumkrümmung unabhängig von Materie beschreibt. Auch Theorien ganz ohne die Existenz von Dunkler Energie existieren und werden überprüft. Aufgrund der Tatsache, dass sich die Dunkle Energie immer und überall mit konstanter Dichte von 10^-26 kg/m³ befindet, ist sie so schwer zu entdecken. Ihre Masse in unserem Sonnensystem entspricht höchstens der Masse eines kleinen Asteroiden und hat somit keine spürbaren Auswirkungen – diese treten erst auf viel größeren Strecken und längeren Zeitspannen auf. Auch weil konkrete experimentelle Einschränkungen fehlen, gestaltet sich der Prozess des Konstruierens von Modellen der Dunklen Energie schwierig. Damit die beschriebene beobachtbare beschleunigte Ausdehnung des Universums durch die Dunkle Energie verursacht werden kann, muss ihr Druck negativ sein. Dies widerspricht zwar unserer Intuition, ist aber möglich. Dieser negative Druck verhindert, dass die Dunkle Energie Strukturen bilden kann – sie muss allerdings in die kosmische Strukturbildung eingreifen können, da sie ja ebendiesen Ablauf der Ausdehnung verändert. Die verschiedenen theoretischen Modelle setzen den Zeitpunkt der Bildung kosmischer Strukturen aus Dunkler Materie unterschiedlich im Rahmen der kosmischen Geschichte, wodurch diese Gebilde auch mehr oder weniger dicht sind [1] [6].

Die bekanntesten Ansätze für Erklärungen der Dunklen Energie lassen sich in fünf Gruppen einteilen und werden im Folgenden kurz zusammengefasst.

Der erste Ansatz geht auf Einsteins Kosmologische Konstante zurück. Diese Erklärung gilt als konservativste für das Wesen der Dunklen Energie und beschreibt diese schlicht als eine Eigenschaft des Raums. Das Weltall würde in Folge dessen auf Grund von Quantenfeldern (Bsp: Higgs-Feld) immer weiter expandieren. Die heute bekannten Theorien sind jedoch noch nicht so weit, als dass sie ein schlüssiges Bild der Wechselwirkungen von Quantenfeldern und der Raumzeit zu liefern [7] [8].

Der zweite Ansatz ist unter dem Stichwort der Quintessenz bekannt. Die Idee ist, dass sich ein neues, unentdecktes Feld ausgedacht wird, welches sich im Vakuum befindet und sich mit der Zeit verändert. Das zugehörige Quantenfeld würde das gesamte Weltall durchziehen und abstoßend wirken. Ein Vorteil der Dynamik dieser Quintessenz ist, dass sie sich im Gegensatz zur kosmologischen Konstante ändern kann, und sich so den gegebenen Rahmenbedingungen anpassen könnte. Die Form, die diese Quintessenz haben könnte, ist völlig unklar [7] [9].

Es haben sich mit der Zeit viele unterschiedliche Theorien entwickelt, mit jeweils unterschiedlichen Eigenschaften des Quantenfeld im Rahmen der Quintessenz-Theorien. Eine der bekannteren ist die Phantomenergie. Diesem Ansatz zufolge ist die Dunkle Energie ebenfalls dynamisch, zusätzlich wird sie mit der Zeit auch noch immer stärker. Diese Theorie beschreibt, dass es aufgrund der immer weiter zunehmenden Ausdehnungsrate irgendwann zu einem „Big Rip“ (Großes Zerreißen) kommen muss, bei dem es schließlich von Sternensystemen bis zu Atomen alles zerreißen würde [7] [10].

Ein weiterer Ansatz ist, dass Dunkle Energie gar nicht Existiert, sondern dass allein der Zerfall Dunkler Materie für die beschleunigte Expansion des Alls verantwortlich ist. Es könnte sich beispielsweise ein leichtes Dunkle-Materie-Teilchen bilden und ein sogenanntes Dunkles Photon würde frei werden. Das Problem mit dieser Idee ist, dass sie zu vielen astrophysikalischen Daten nicht passt [7].

Der letzte Ansatz, der an dieser Stelle vorgestellt werden soll, ist der, dass eventuell unser generelles Verständnis von Raumzeit und Gravitation nicht stimmt. Es wurden Modelle aufgestellt, bei denen zusätzliche Felder die Gravitation im Weltall verändern sollen, welche dann wiederrum die der Dunklen Energie zugeschriebene Wirkung erklären sollen. Auch bei diesem Ansatz ist das Problem, dass er zu vielen astrophysikalischen Erkenntnissen nicht passt [7].

[1] Dunkle Energie, Welt der Physik (Link: https://www.weltderphysik.de/gebiet/universum/dunkle-energie/), aufgerufen am 15.06.2020

[2] Dunkle Energie, Lexikon der Astronomie, Spektrum (Link: https://www.spektrum.de/lexikon/astronomie/dunkle-energie/83), aufgerufen am 15.06.2020

[3] Turner, Michael S.: Dark Matter and Dark Energy in the Universe, The Third Stromlo Symposium: The Galactic Halo; ASP Conference Series, Vol. 165, 1999

[4] Huterer, Dragan; Turner, Michael S.: Prospects for probing the dark energy via supernova distance measurements; Phys. Rev. D 60, 081301; 30.08.1999

[5] Perlmutter, Saul; Turner, Michael S.; White, Martin: Constraining Dark Energy with Type Ia Supernovae and Large-Scale Structure; Phys. Rev. Lett. 83, 670; 26.07.1999

[6] Conselice, Christopher: Die unsichtbare Hand des Universums, Spektrum der Wissenschaft, 4/07

[7] Eidemüller, Dirk: Fünf Erklärungen für die Dunkle Energie (Link: https://www.spektrum.de/news/fuenf-erklaerungen-fuer-die-dunkle-energie/1740008), aufgerufen am 09.07.2020

[8] Peebles, P. J. E.; Ratra, Bharat: The cosmological constant and dark energy; Rev. Mod. Phys. 75, 559; 22.04.2003

[9] Zhang, Jingfei; Zhang, Xin; Liu, Hongya: Agegraphic dark energy as a quintessence, The European Physical Journal C 54; 2008

[10] Briscese, F.; Elizalde, E.; Nojiri, S.; Odintsov, S. D.: Phantom scalar dark energy as modified gravity: Understanding the origin of the Big Rip singularity; Physics Letters B, Volume 646; 08.03.2007

Die Theorie der Modifizierten Newtonschen Dynamik oder auch MOND-Theorie genannt, beschreibt eine alternative Gravitationstheorie, in welcher das Rotationsverhalten von Galaxien durch Modifikationen der Bewegungsgleichungen der Materie im Gravitationsfeld erklärt werden soll. Entwickelt wurde sie im Jahre 1983 von dem israelischen Physiker Mordehai Milgrom als Alternative zu der Dunklen Materie und wird seither weiterentwickelt und modifiziert [1] [2] [3] [4].

Die Motivation für die MOND-Theorie waren in den 1980er Jahren gemessene Abweichungen der Rotation von Galaxien von den Erwartungen im Rahmen der Newtonschen Gravitationstheorie, welche bei der Bewegung von Gaswolken in rotierenden Scheiben von Spiralgalaxien festgestellt wurden. Gemessene Rotation sowie Zufallsbewegungen sind größer als zuvor erwartet, d.h. es treten durch Newton nicht erklärbare Beschleunigungsvariationen auf. Auch bei den Sonden Pioneer 10 und 11 konnten unerwartete Beschleunigungen festgestellt werden. Außerdem konnte bis heute keine nicht-baryonische Materie, also nicht sichtbare Materie, gefunden werden [1] [2] [5] [6] [7].

Diese Abweichungen können in der konventionellen Astrophysik durch die sogenannte Dunkle Materie aufgelöst werden, nachdem diese eine zusätzliche Gravitationskraft erzeugt, welche die Beschleunigungen erklärbar macht. Diese Theorie beschreibt eine kugelige Verteilung der Dunklen Materie um die Scheibe der Spiralgalaxien, auch Dunkle Materie Halo genannt, welche die beobachteten Rotationskurven gut erklärt.

Die Theorie der Modifizierten Newtonschen Dynamik stellt eine alternative Erklärung der Phänomene ohne die Existenz Dunkler Materie dar. Der Ansatz lautet

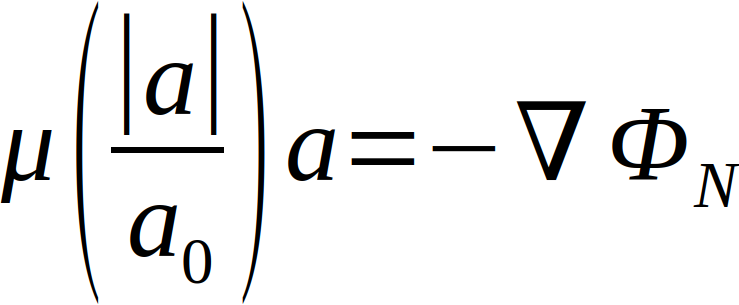
mit der Beschleunigung a, der Modifikation µ und auf der rechten Seite mit dem negativen Gradienten des Gravitationspotentials Φ_N . Bei einem Modifikationswert von µ=1 ergibt sich der Fall der klassischen Newtonschen Gravitation. Milgrom setzt nun eine glatte und beschleunigungsabhängige Funktion µ an. Bei |α| >> α₀ geht die Funktion gegen 1, wobei α₀ eine Konstante mit 1,2 *10^-10 m/s²beschreibt.

Die MOND-Theorie ist konsistent mit der Tully-Fisher-Relation sowie mit der beobachteten Abflachung der Rotationskurven in Spiralgalaxien. 1984 wurde die Theorie von Milgrom und Jacob Bekenstein mit Hilfe eines Lagrange-Funktionals zu der AQUAL-Theorie (Aquadratic Lagrangian Theory) weiterentwickelt. Diese ist konsistent mit dem schwachen Äquivalenzprinzip [8] [9] [10].

Generell wird diese Theorie sehr kontrovers diskutiert. Erik Verlinde, ein niederländischer Physiker, hat die Theorie in den letzten Jahren ebenfalls weiterentwickelt, nach derer sowohl die Dunkle Materie als auch die Gravitation eine Folge der Dunklen Energie seien.

[1] Spektrum: Lexikon der Astronomie: MOND; (Link: https://www.spektrum.de/lexikon/astronomie/mond/305), aufgerufen am 11.05.2020

[2] Physik Cosmos-indirekt; Modifizierte Newtonsche Dynamik; (Link: https://physik.cosmos-indirekt.de/Physik-Schule/Modifizierte_Newtonsche_Dynamik), aufgerufen am 13.05.2020

[3] Milgrom, Mordehai: MOND: time for a change of mind? (08/2009)

[4] Milgrom, Mordehai: New Physics at Low Accelerations (MOND): an Alternative to Dark Matter

[5] Milgrom, Mordehai: Dynamics with a non-standard inertia acceleration relation: an alternative to dark matter; Ann. Phys. 229, 1994 (Link: doi:10.1006/aphy.1994.1012), arXiv, aufgerufen am 20.08.2020

[6] Anderson, John D.; Laing, Philip A.; Lau, Eunice L.; et. Al.: Study of the anomalous acceleration of Pioneer 10 and 11

[7] Sanders, R. H.: The Published Extended Rotation Curves of Spiral Galaxies: Confrontation with Modified Dynamics; The Astrophysical Journal, Volume 473, Number 1; 1996

[8] Steinmetz, Matthias; Navarro, Julio F.: The Cosmological Origin of the Tully-Fisher Relation, 1999

[9] Bekenstein, Jacob D.: Relativistic gravitation theory for the modified Newtonian dynamics paradigm, Phys. Rev. D 70, 10/2014

[10] Bekenstein, Jacob D.: Modified Gravity vs Dark Matter: Relativistic theory for MOND, 06/2004

Weiterführende Literatur:

[11] Bekenstein, Jacob D.: Modified gravity as an alternative to dark matter (01/2010)

[12] Famaey, B.; McGaugh, S.; Milgrom, M.: MOND and the dynamics of NGC1052-DF2 (04/2018)

[13] Milgrom, Mordehai: Light and Dark in the Universe (03/2012)

[14] Milgrom, Mordehai: MOND laws of galactic dynamics (12/2012)

[15] Bekenstein, Jacob D.: The modified Newtonian dynamics – MOND – and its implications for new physics; Contemporary Physics 47; 2006

[16] Bekenstein, Jacob; Milgrom, Mordehai: Does the missing mass problem signal the breakdown of Newtonian gravity?; Astrophysical Journal Part I, vol. 286; 1984

Die Größe der Erdanziehung bzw. Schwerebeschleunigung g ist von der Masseverteilung in der Erde abhängig. Je mehr Masse bis zum Erdmittelpunkt unter einem ist oder je höher die Dichte dieser Masse, desto höher die Anziehungskraft. Mit einem Gravimeter kann die lokale  Erdbeschleunigung gemessen werden. Daraus lassen sich Rückschlüsse auch auf die  Beschaffenheit des Untergrundes ziehen, z.B. Hohlräume oder Erzlager erkennen.
Die Schwerebeschleunigung hängt von der geografischen Breite und der Höhe über Meeresniveau  ab. Auf Meereshöhe ist am Äquator g=9,780 m/s^2, am 45ten Breitengrad g=9,807 m/s² und am Pol  g=9,832 m/s². Mit jedem zusätzlichen Höhenmeter nimmt g um etwa 3*10 ^-6 m/s² ab, solange h klein gegen den  Erdradius ist.
Am Äquator ist der Abstand vom Erdmittelpunkt größer und damit die Schwerebeschleunigung  geringer als an den Polen.
Zusätzlich wirkt die Fliehkraft aufgrund der Erdrotation der Fallbeschleunigung entgegen, so dass diese am Äquator geringer ist. Der Effekt beträgt etwa 3 Gal.
Die lokalen Absolutwerte der Erdbeschleunigung können bei den Landesvermessungsämtern  erfragt werden.

Gezeiten entstehen durch die Rotation von Erde und Mond um den gemeinsamen  Massenschwerpunkt. Entscheidend sind die Differenzkräfte zwischen Gravitations- und  Fliehkräften. Diese sorgen dafür, dass sich auf der Erde sowohl auf der dem Mond  zugewandten, als auch auf der dem Mond abgewandten Seite ein Flutberg ausbildet. Daher gibt  es zweimal am Tag Ebbe und Flut. Zusätzlich übt auch die Sonne einen Einfluss auf die  Gezeiten aus, woraus durch Addition bei Neu und Vollmond Springfluten und durch Subtraktion bei  Halbmond Nippfluten entstehen.
Die Gezeitenkräfte lassen sich, auch unabhängig vom Tidenhub der Meere, mit einem Gravimeter  an jedem Ort der Erde messen. Sie liegen in der Größenordnung von 0,5 mGal bis 1,1 mGal.

Die Gravitationskonstante G stammt aus dem Newtonschen Gravitationsgesetz und beschreibt die Anziehungskraft zweier Körper der Massen m₁ und m₂ im Schwerpunktsabstand r über die Formel

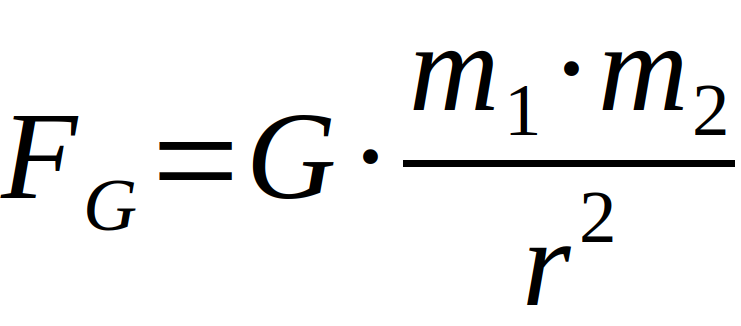
Da sie die schwächste der bekannten Wechselwirkungen ist und sich nicht abschirmen lässt, ist sie die mit der geringsten Genauigkeit gemessene Naturkonstante [1], [2], [3].

Im Jahr 1798 wurde die Gravitationskonstante erstmals von Cavendish bestimmt [2], [4]. Seither wurden mehr als 300 Versuche vorgenommen, doch selbst jüngste Messungen weisen Abweichungen von bis zu 0,055 % auf. Besonders für die Quantengravitation würden genauere Ergebnisse der Messungen neue Möglichkeiten eröffnen.

1998 wurden anlässlich einer „Zweihundertjahrfeier“ der ersten Messung der Gravitationskonstante die Ergebnisse der G-Messungen von 12 Forscherteams mit jeweils sehr unterschiedlichen Apparaturen verglichen. Die Genauigkeit ist in der folgenden Tabelle in ppm angegeben [5], [6].

Labor	G * 1011	(ppm)
New Zealand MSL	6,6742(6)	90
Zürich	6,6749(14)	210
Wuppertal	6,6735(9)(13)	240
JILA	6,6873(94)	1400
BIPM	6,683(11)	1650
Karagioz (Russia)	6,6729(5)	75
Luther/ Towler	6,6726(5)	64
PTB	6,71540(56)	83

Es ist zu erkennen, dass die verschiedenen Institute zwar mit einer Genauigkeit von 0,001 % gemessen haben, die Ergebnisse jedoch um bis zu 0,5 % voneinander abweichen.

Dieser Vergleich und die sich ergebenen Diskrepanzen resultierte im Jahr 2000 in einer Reihe neuer Messungen und neuer Experimente. Die Forscher Steve Merkowitz und Jens Gundlach entwickelten daraufhin einen Cavendish Apparat, mit dem sie die Ungenauigkeit um einen Faktor 10 senken konnten. Ihr Apparat folgte grundlegend dem Aufbau der Cavendish Torsionswaage, allerdings bauten sie einen zusätzlichen Rückkopplungsmechanismus ein, um die Testmassen zu bewegen, und somit die Verdrillung des Pendels auf ein Minimum zu beschränken [7], [8].

Nach ihren Ergebnissen liegt der Wert der Gravitationskonstante bei

mit einer Unsicherheit von 0,0014 % [2], [7]. Diese Messung ermöglichte, gemeinsam mit Daten des Lageos Satelliten, die bis dahin genaueste Bestimmung der Erd- und der Sonnenmassen [2], [3].

Aufgrund der vielen Messungen, die in den letzten 25 Jahren vorgenommen wurden und den Diskrepanzen, die die Ergebnisse mit sich brachten, legte das Committee on Data for Science and Technology (CODATA) 2014 den vorgeschlagenen Wert für die Gravitationskonstante auf

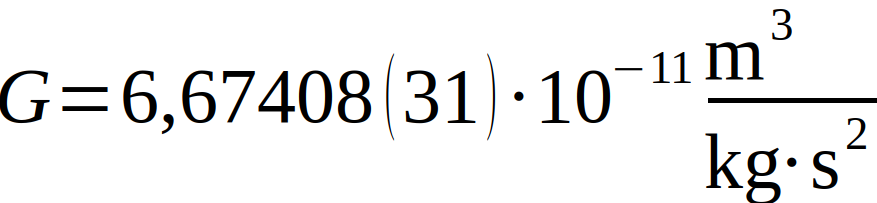
mit einer Unsicherheit von 0,0047 % [9].

Es ist nicht auszuschließen, dass die Abweichungen der Messungen ihren Ursprung in unentdeckten Eigenschaften der Gravitation haben, allerdings ist das eher unwahrscheinlich. Wahrscheinlicher ist es, dass bisher unentdeckte systematische Fehler eine genauere Bestimmung verhindern [3].

Im Rahmen von Messreihen an der Bergischen Universität Wuppertal wurden als primäre Fehlerquellen der Messungen der sogenannte Choke-Effekt (der Effekt, dass Variationen des Abstandes zwischen dem Spiegel und dem Drosselflansch zu Änderungen der Resonanzfrequenz führen), die Neigung des Stützgerüstes aufgrund der Deformation des Fundamentes durch die Testmassen sowie die Positionierung der Testmassen genannt [1].

2018 konnten chinesische Forscher durch Änderungen zweier Experimentaufbauten die Ungenauigkeit der Messungen erneut reduzieren. Beim Ersten Aufbau hing ein vergoldeter Quarzblock an einer Glasfaser und zwei 778 g schwere Stahlkugeln waren die Testmassen. Beim zweiten Versuch befanden sich Torsionspendel und Stahlkugeln auf je einem Drehtisch, damit sie unabhängig voneinander rotieren können und die Verdrillung des Fadens so unterbunden werden kann. Aus diesen beiden Versuchen ergaben sich zwei unterschiedliche Werte für die Gravitationskonstante, beide in dem der CODATA festgelegten Bereich. Die Unsicherheit von 0,0047 % konnte somit auf 0,0012 % gesenkt werden. Warum die beiden Werte der chinesischen Experimente trotzdem recht stark voneinander abweichen, ist immer noch unklar [10], [11].

[1] Kleinevoß, Ulf: Bestimmung der Newtonschen Gravitationskonstanten G; Bergische Universität Gesamthochschule Wuppertal

[2] LEIFIphysik Joachim Herz Stiftung: Gravitationsgesetz und -feld: Ausblick Gravitationskonstante (Link: https://www.leifiphysik.de/mechanik/gravitationsgesetz-und-feld/ausblick/gravitationskonstante), aufgerufen am 25.06.2020

[3] Makro und Mikrokosmos: Berechnung der Gravitationskonstante G (Link: https://www.makro-und-mikrokosmos.de/berechnung-der-gravitationskonstante-g-aus-drei-naturkonstanten-der-quantenphysik/), aufgerufen am 25.06.2020

[4] Cavendish, Henry: XXI. Experiments to determine the Density of the Earth, 21.06.1798

[5] Kestenbaum, David: Gravity Measurements Close in on Big G, 18.12.1998

[6] Newman, Riley: Convergence (?) of G Measurements – Mysteries Remain, University of California, 03.2003

[7] Physics central: Big ‚G‘ (Link: https://www.physicscentral.com/explore/action/bigg.cfm), aufgerufen am 25.06.2020

[8] Gundlach, Jens H.; Merkowitz, Stephen M.: Measurement of Newton’s Constant Using a Torsion Balance with Angular Acceleration Reedbach, Phys. Rev. Lett. 85, 2869; 02.10.2000

[9] Mohr, Peter; Newell, David; Taylor, Barry: CODATA Recommended Values of the Fundamental Physical Constants: 2014

[10] Scharf, Rainer: Gravitationskonstante genauer denn je gemessen (Link: https://www.pro-physik.de/nachrichten/gravitationskonstante-genauer-denn-je-gemessen), aufgerufen am 25.06.2020

[11] Wu, Junfei; Li, Qing; Liu, Jianping; et. Al.: Progress in Precise Measurements of the Gravitatinal Constant, Annalen der Physik, Volume 531, 08.04.2019

Weiterführende Literatur:

[12] Wolschin, G.: Schwierige Bestimmung einer fundamentalen Naturkonstante

[13] Schlamminger, S.; Gundlach, J.H.; Newman, R.D.: Recent measurements of the gravitational constant as a function of time, Phys. Rev. D 91, 11.06.2015

[14] Newman, Riley D.: The Challenge of Measuring G, The Ninth Marcel Grossmann Meeting, 2002

“Groß G” ist die Proportionalitätskonstante in Newtons Gravitationsgesetz. Sie stellt eine formale Beziehung her zwischen den Massen, dem Abstand und der daraus resultierenden  Gravitationskraft. Inzwischen wird vermutet, dass G nicht konstant ist, sondern von  weiteren, bisher unbekannten Faktoren abhängen könnte.

Anerkannter CODATA-Wert 2010 ist:
G = ( 6,67348 ± 0,00080 ). 10 ^-11 m³ kg^-1 s^-2. Die Genauigkeit dieses Wertes beträgt nur 0,15 %, was für eine  Fundamentalkonstante sehr ungenau ist.

“Klein g” bezeichnet die Beschleunigung, mit der ein frei fallender Körper im  Gravitationsfeld der Erde an Geschwindigkeit zunimmt. Durchschnittlicher Wert: g = 9,80665 m/s² (CODATA-Wert 2010).

Gal steht für Galileo und ist eine andere Einheit für die Erdbeschleunigung g, die vor allem  in der Geophysik verwendet wird. Es ist 1 Gal =10 ^-2 m/s², also g=981 Gal. Für die Beschreibung kleiner Effekte wird meistens mGal=0,001 Gal verwendet.

Die Cavendish-Waage (auch Gravitationswaage genannt) beruht auf einem Experiment des Wissenschaftlers Henry Cavendish, welches im Jahr 1798 das erste Mal durchgeführt wurde. Cavendishs eigentliches Ziel war es, die Dichte der Erde bestimmen zu können – er interessierte sich selbst nicht für die Gravitationskonstante, es gelang durch sein Experiment trotz dessen, den Wert der von Isaac Newton in seinem Gravitationsgesetz beschriebene Gravitationskonstante G, annähernd genau zu errechnen [1], [2].

Im Wesentlichen handelt es sich bei der Cavendish-Waage um eine Drehwaage, die auf der auf einen Draht aufgebrachten Torsionskraft beruht, d.h. der Betrag des Winkels, um den dieser Draht ausgelenkt wird, gibt Auskunft über das wirkende Drehmoment und die zwischen den Testmassen wirkende Kraft lässt sich berechnen. Genauer bedeutet das, dass sich in der Mitte der Waage ein Draht befindet, an dessen Ende ein waagerechter Stab angebracht ist. An dessen Mitte ist ein Spiegel und an dessen Enden jeweils eine kleine Masse befestigt. Davor befindet sich eine Lichtquelle, welche einen möglichst konzentrierten Lichtstrahl emittiert, heutzutage z.B. ein Laser. Dieser Lichtstrahl ist auf den Torsionsdraht gerichtet und wird von dem Spiegel auf einen Schirm reflektiert. Sobald nun eine Auslenkung der Massen aus der Ruhelage geschieht, verschiebt sich der Lichtpunkt [1].

Um das Experiment durchzuführen, werden nun zwei große Massen M im gleichen Abstand r zu den kleineren Massen positioniert. Die Massen m und M auf den gegenüberliegenden Seiten ziehen sich an und der Stab mitsamt dem Spiegel wird sich leicht verdrehen – der Lichtpunkt wird sich auf dem Schirm um die Strecke s0 bewegen und das System gerät in eine gedämpfte Schwingung. Anschließend wird der Stab mit den schweren Massen um fast 180° gedreht, wodurch sich der Effekt umkehren wird und die Auslenkung in die entgegengesetzte Richtung auftritt.

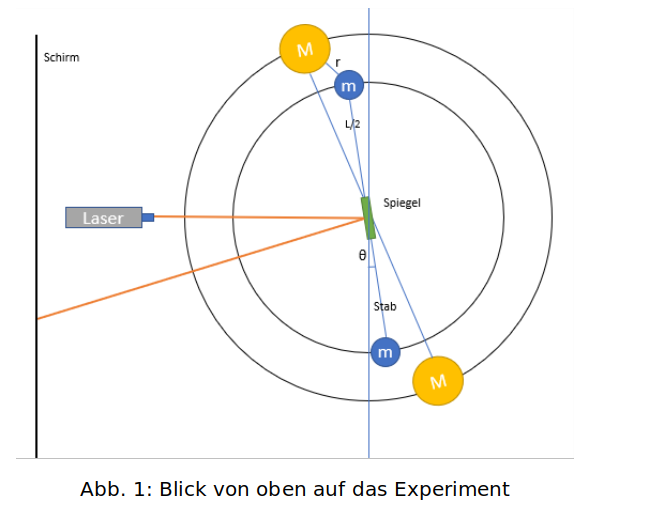
Um die Gravitationskonstante zu erhalten bzw. zu berechnen, müssen nun die Hebellänge des Stabes L, die Entfernung zum Schirm S sowie die Masse M bekannt sein. Unter der Annahme, dass die Abstände zwischen den kleinen und großen Massen klein gegenüber der gesamten Systemgröße sind, ergibt sich für das auftretende Drehmoment an der Stange

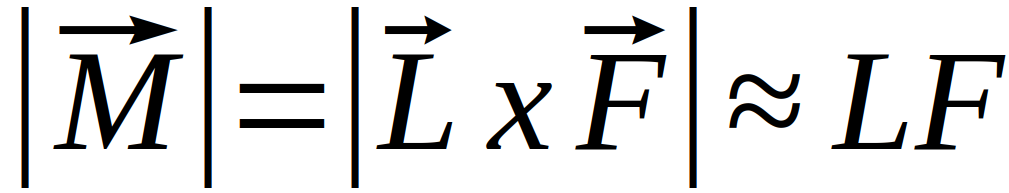
Durch die Anziehung der Massen mit kleinem Abstand r wird ein Drehmoment erzeugt, welches auf den Stab wirkt und sich nach folgender Formel ergibt

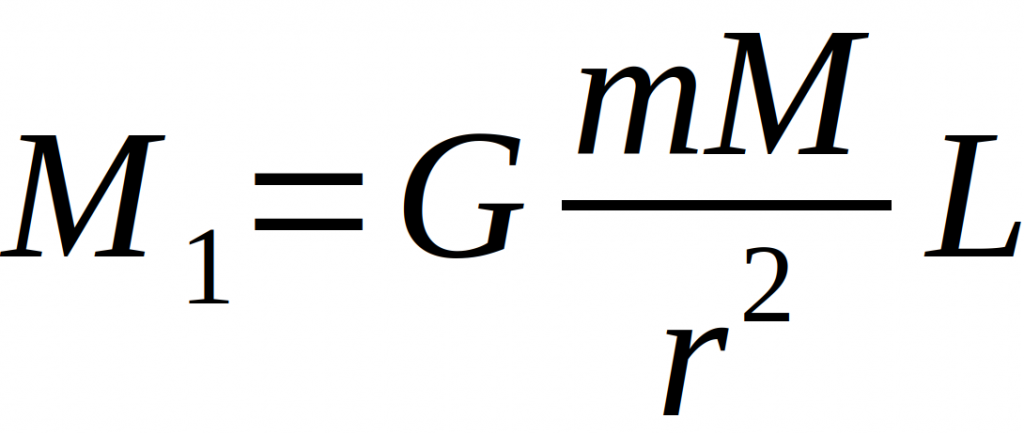
Auch die jeweils gegenüberliegende große Masse M bewirkt eine Kraft auf die jeweilige andere kleine Masse nach

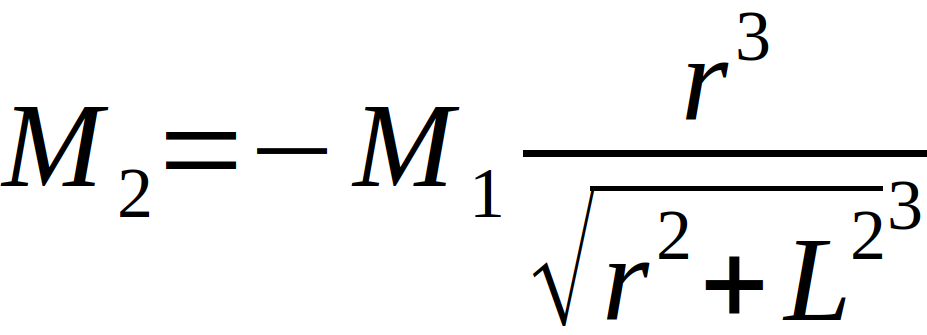
Das resultierende Drehmoment M_res ergibt sich aus der Summe von M₁ und M₂, die korrespondierende Gegenkraft ist die Festigkeit des Drahtes, welche sich aus dem Direktionsmoment D und dem Winkel Theta ergibt. Es gilt also

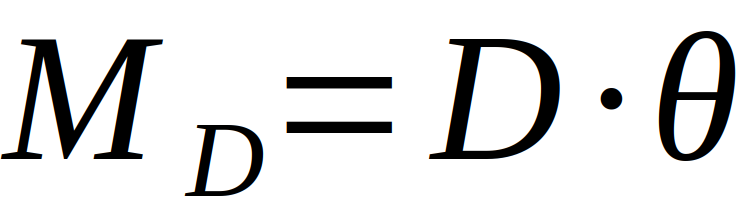
Beziehungsweise für das Kräftegleichgewicht

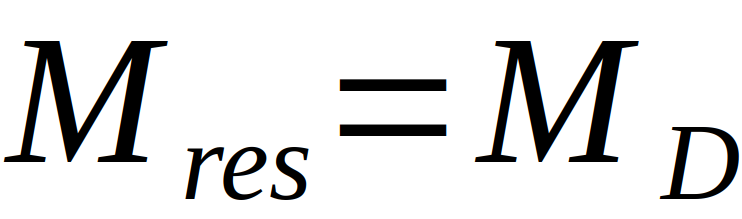
Dadurch, dass Drehschwingungen in der linearen Näherung harmonisch sind, ist die Kreisfrequenz Omega nur abhängig von dem Direktionsmoment D und dem Trägheitsmoment. Das Trägheitsmoment lässt sich direkt nach

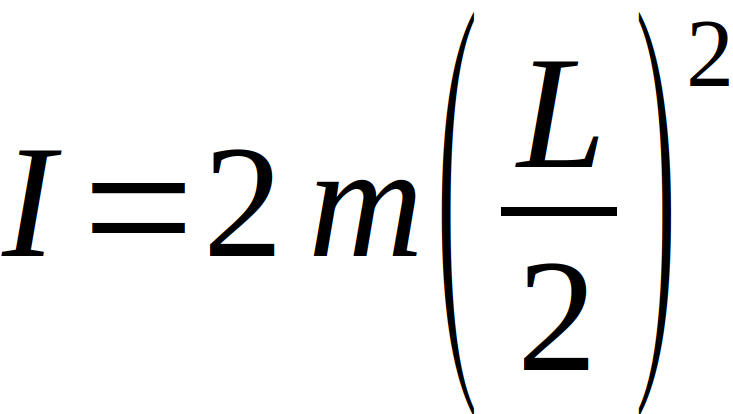
bestimmen. Mit diesem Wert sowie der Formel für die Schwingungsdauer

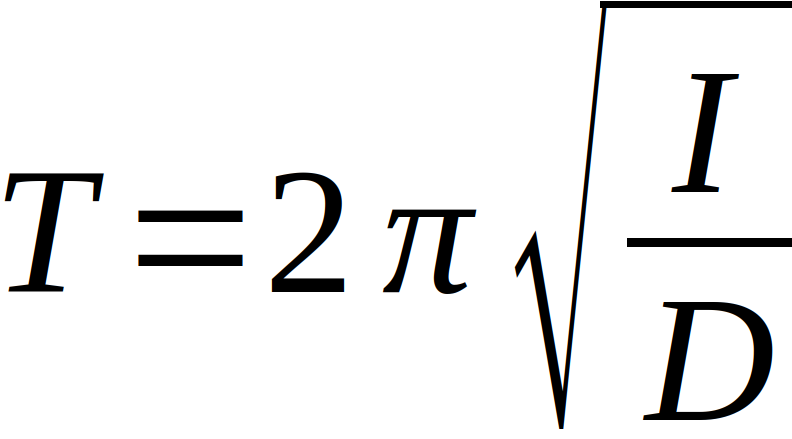
lässt sich direkt auf das gesuchte Direktionsmoment D schließen. Es ergibt sich

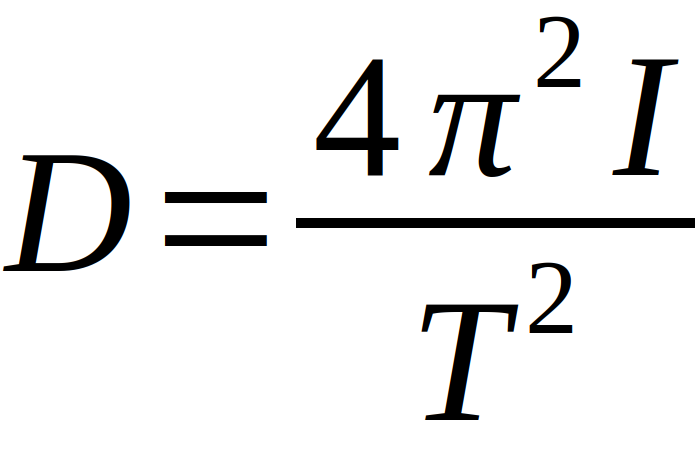
Der Drehwinkel Theta, welcher ebenfalls in die Gegenkraft M_D eingeht, ergibt sich über die Auslenkung des Spiegels, denn es gilt generell bei allen Spiegeln: Der Drehwinkel der Abbildung ist doppelt so groß, wie der Drehwinkel des Spiegels selbst. Bei der Annahme eines leicht gewölbten Schirms ergibt sich für den Winkel

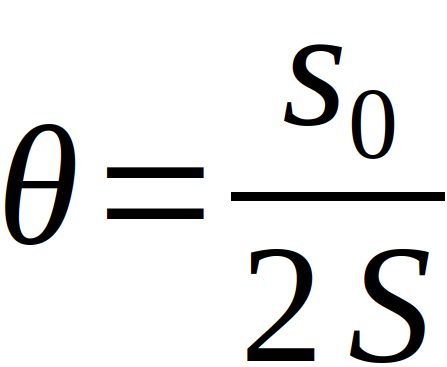
Setzt man diese Erkenntnisse nun in das Kräftegleichgewicht ein, kann nach der Gravitationskonstante umgeformt werden und es ergibt sich [1], [2]

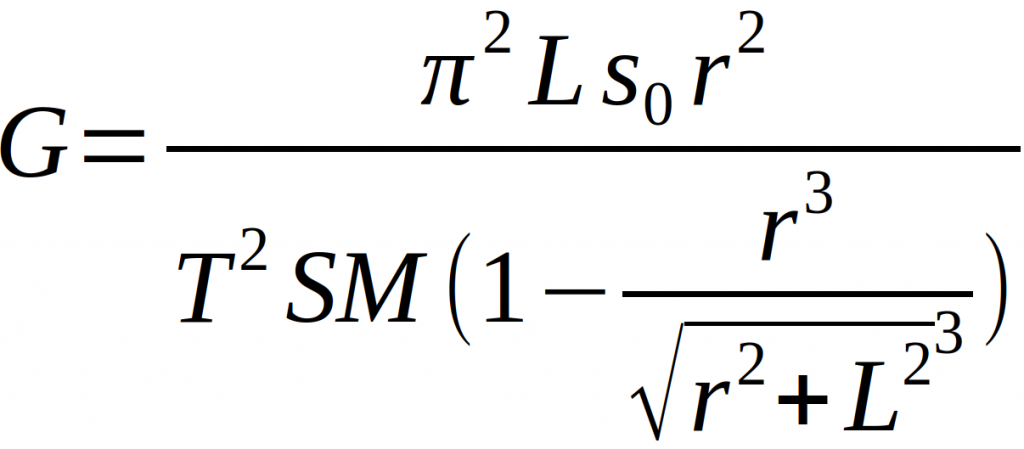
Henry Cavendish war es somit als erstem möglich, die Gravitationskonstante mit hoher Genauigkeit zu bestimmen. Sein Ergebnis lautete

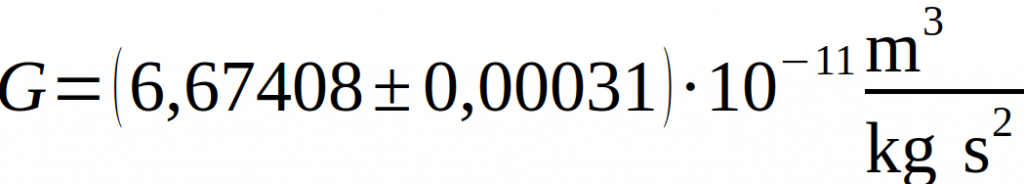
Durch die spezielle Konstruktion der Gravitationswaage können sehr kleine Kräfte gemessen werden, weshalb sie neben den beschriebenen Experimenten auch für weitere Entdeckungen genutzt wurde, wie z.B. die Bestimmung der Coulombkraft elektrisch geladener Körper.

[1] Physik Cosmos (Link: https://physik.cosmos-indirekt.de/Physik-Schule/Gravitationswaage), aufgerufen am 05.05.2020

[2] Cavendish, Henry: XXI. Experiments to determine the Density of the Earth; 21.06.1798; (Link: https://upload.wikimedia.org/wikipedia/commons/0/0b/Cavendish-Experiments_to_Determine_the_Density_of_the_Earth..pdf)

[3] Rundel, Michael, et al.: Physik Libre, 2020

Weiterführende Literatur:

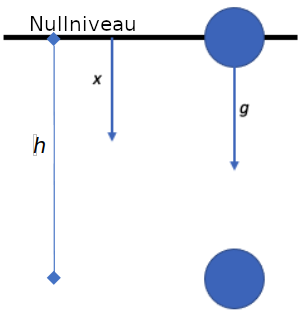
[4] Panov, V. I.; Frontov, V. N.: The Cavendish experiment at large distances; 25.05.1979, Moscow State University

[5] Al Balushi, Abdulrahim; Cong, Wan; Mann, Robert B.: Optomechanical quantum Cavendish; Phys. Rev. A 98, 043811, 05.10.2018

[6] Mostepanenko, V. M.; Sokoliv, I. Yu.: New restrictions on the parameters of the spin-1 antigravitation following from the Casimir effect, Eötvös and Cavendish experiments; Physics Letters A, Volume 132, 17.10.1988

[7] Clotfelter, B. E.: The Cavendish experiment as Cavendish knew it; American Journal of Physics 55; 04.06.1998

[8] Brill, Dieter: The Cavendish Experiment in General Relativity; In: Harvey A. (eds) On Einstein’s Path; Springer, New York, 1999

Der freie Fall in seiner allgemeinen Form, also unter Vernachlässigung von Effekten wie Auftrieb, Luftreibung oder Corioliskraft beschreibt in der klassischen Mechanik die Bewegung eines sich anfangs in Ruhe befindlichen Körpers senkrecht und mit konstanter Erdbeschleunigung g (in Deutschland circa 9,81 m/s²). Werden das Null-Niveau und die Koordinatenrichtung x wie im folgenden Bild in Richtung der Beschleunigung g gewählt, so ergeben sich im einfachsten Fall die nachfolgend aufgeführten Formeln für die Geschwindigkeit v(t), die Position x(t) und bei gegebener Fallhöhe h = x(t=0) die Fallzeit t(h) und die Geschwindigkeit v(h) [1], [2].

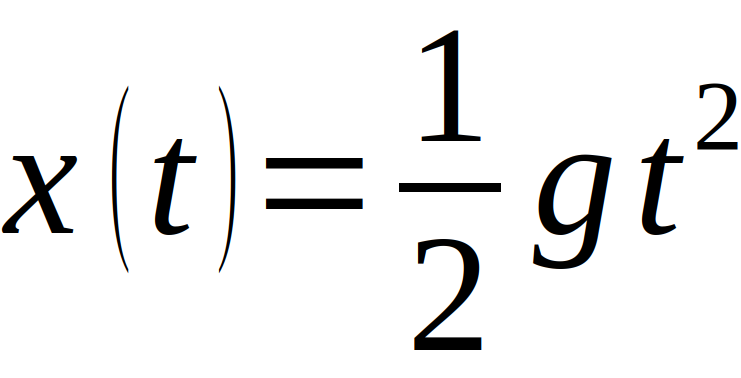
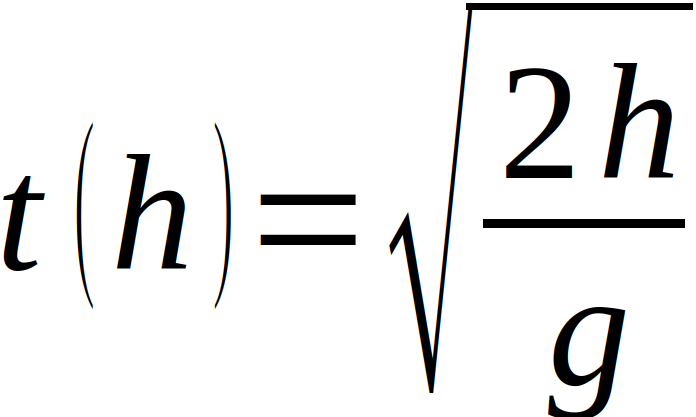
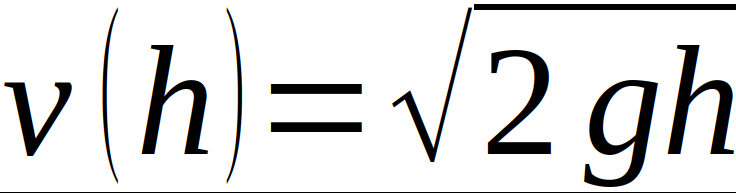
In einigen Fällen ist die Vernachlässigung der Reibungskräfte akzeptabel, im Allgemeinen jedoch eine unrealistische Näherung, denn genau sie bewirkt, dass verschiedene Körper unterschiedlich schnell fallen. Die Formel der Reibungskraft beim freien Fall lautet

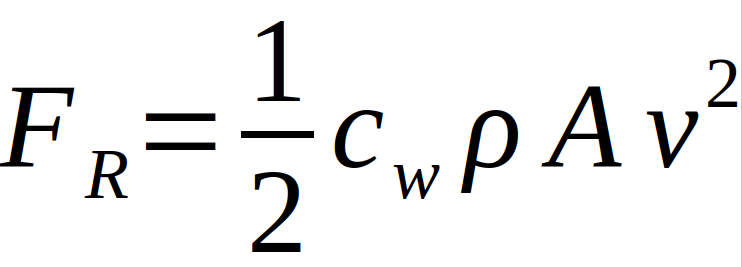
Wobei c_W der sogenannte Widerstandsbeiwert ist, ρ die Dichte des Mediums (bei Luft bspw. 1,23 kg/m³), A die Querschnittsfläche des fallenden Körpers und v die Geschwindigkeit ist. Auffällig ist, dass die Reibungskraft abhängig von der Geschwindigkeit des Körpers ist, die Beschleunigung sich also ändert und somit keine gleichmäßig beschleunigte Bewegung mehr vorliegt [1], [2].

Auf den frei fallenden Körper wirken also entgegengesetzte Kräfte: Die Gewichtskraft zum einen und die ihr entgegengesetzte Widerstandskraft. Durch Gleichsetzen dieser Kräfte lässt sich die Maximalgeschwindigkeit berechnen, welche sich zu

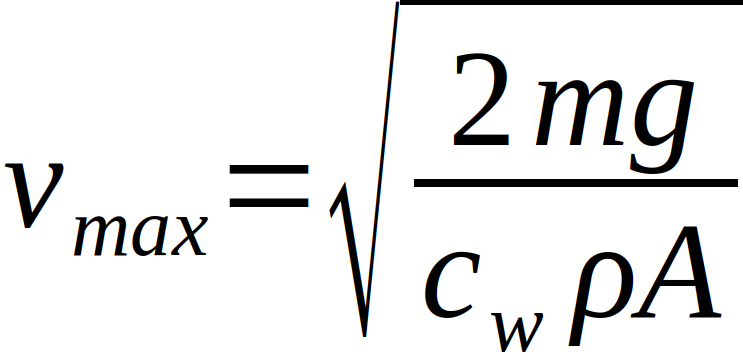
ergibt. Verringern kann sich diese durch Erhöhung der Fläche A oder des Widerstandsbeiwerts c_w.

Die Gleichungen für v(t) und x(t) können nicht mehr in ihrer einfachen Form angewandt werden. Die Bewegungsgleichung des freien Falls unter Berücksichtigung der Reibungskräfte ergibt sich zu

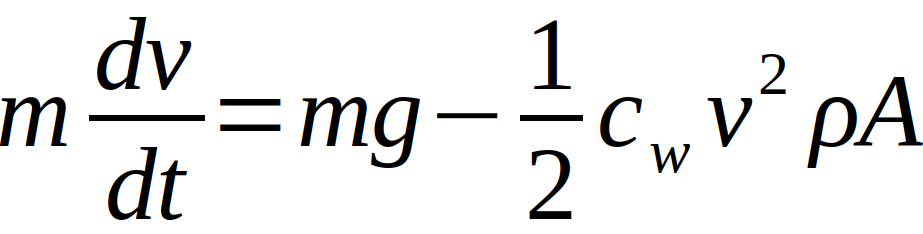
Mit Hilfe der Trennung der Variablen und geschickter Umformung und mit der Anfangsbedingung v(t=0)=0 ergibt sich als Gleichung für die Geschwindigkeit

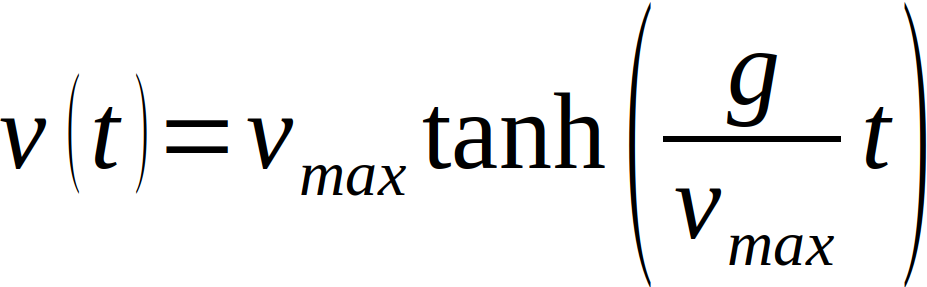
Integriert man nun die Geschwindigkeitsgleichung über die Zeit erhält man die Ortsfunktion

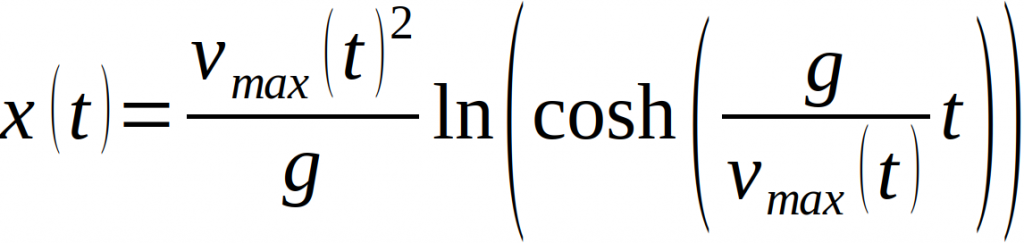
Analog können neben der Luftreibung auch Kräfte wie z.B. Auftriebskräfte berücksichtigt werden. Die Auftriebskraft berechnet sich aus der Dichte des Mediums, durch den der Körper fällt ρ₀ , dem Volumen des Körpers sowie der Erdbeschleunigung [2]:

[1] Physik Cosmos: Fall mit Luftwiderstand, (Link: https://physik.cosmos-indirekt.de/Physik-Schule/Fall_mit_Luftwiderstand), aufgerufen am 09.11.2020

[2] Leifiphysik: Freier Fall – Senkrechter Wurf, (Link: https://www.leifiphysik.de/mechanik/freier-fall-senkrechter-wurf/grundwissen/freier-fall), aufgerufen am 13.11.2020

[3] Gross, Dietmar; Hauger, Werner; Schröder, Jörg; Wall, Wolfgang A.: Technische Mechanik; 13. Auflage; 2016

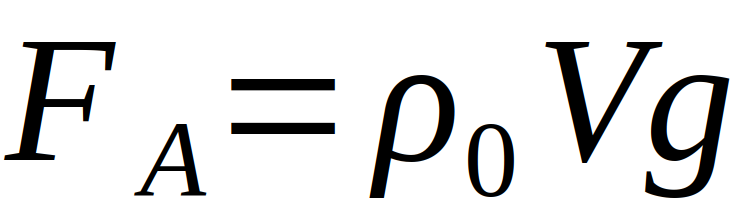
Weiterführende Literatur:

[4] Wunderlich, Daniel: Bewegungen – Freier Fall eines Massenpunktes, 25.11.2008

[5] Wolf, K.: Lehrbuch der Technischen Mechanik starrer Systeme, 1947, Springer-Verlag, Wien

Ein Parakonisches Pendel ist ein spezielles physikalisches Pendel, mit welchem der gravitative Einfluss anderer Himmelskörper (z.B. Mond und Sonne) auf die Pendelbewegung gemessen werden soll. Im Aufhängepunkt befindet sich eine Kugel, welche bei jeder Pendelbewegung auf einer Ebene abrollt und statt eines Fadens, wie bei vielen anderen Pendeln, handelt es sich bei einem parakonischen Pendel um einen starren Stab, an welchem der Pendelkörper befestigt ist. Die Pendellänge ist typischerweise circa 1 m. Aufgrund seines speziellen Aufbaus besitzt das Pendel einen Freiheitsgrad mehr als andere, da es auch Drehungen um die Längsachse durchführen kann [1], [2].

Grundsätzlich werden Fadenpendel in zwei Gruppen aufgeteilt: Mathematische Pendel und physikalische Pendel. Mathematische Pendel sind idealisierte Fadenpendel mit den Annahmen des nicht-dehnbaren Fadens mit vernachlässigbarer Masse, einer reibungsfreien Aufhängung des Pendels und einer punktförmigen Masse des Pendelkörpers. Physikalische Pendel sind starre Körper, die unter der Wirkung der Schwerkraft Drehbewegungen um eine feste Achse, welche nicht durch den Schwerpunkt geht, ausführen. Versucht man das parakonische Pendel einzusortieren stellt man fest, dass es sich zwar vom Aufbau her um ein physikalisches Pendel handelt, die Gleichungen teilweise jedoch von denen mathematischer Pendel hergeleitet wurden [3].

Beim parakonischen Pendel handelt es sich demnach nicht um ein mathematisches Pendel, die Kreisfrequenz ω bzw. die Periodendauer T folgt trotzdem recht gut der Formel der mathematischen Pendel nach

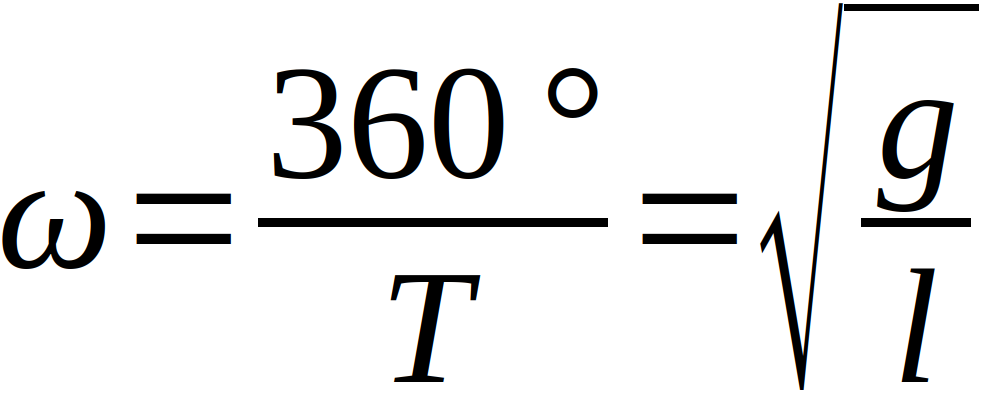
Wird das Pendel ausgelenkt, legen der Pendelstab und der Pendelkörper eine Bewegung in Form eines Kegels mit nahezu elliptischer Basis zurück. Diese Ellipse wird im Folgenden mit Länge A und Breite a beschrieben.

Die Winkelgeschwindigkeit des Pendelkörpers in der xy-Ebene wird beschrieben durch

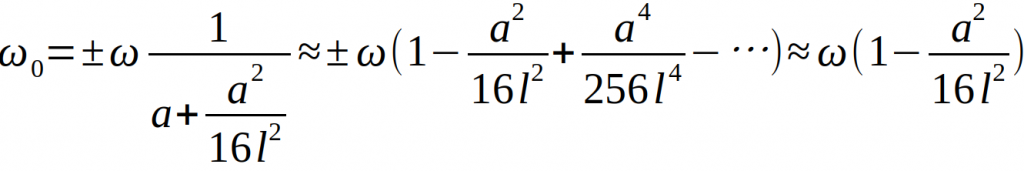
Der Physiker G. B. Airy fand heraus, dass sich die Bahnellipse der Pendelkörpers je nach Form der Ellipse, also je nach Größenunterschied zwischen A und a mehr oder weniger langsam um die z-Achse drehen muss. Dieser Effekt wird Airy-Effekt genannt. Wird nun ein Drehwinkel ϕ_Airy definiert, so ergibt sich die Winkelgeschwindigkeit dieser Drehung nach [1]

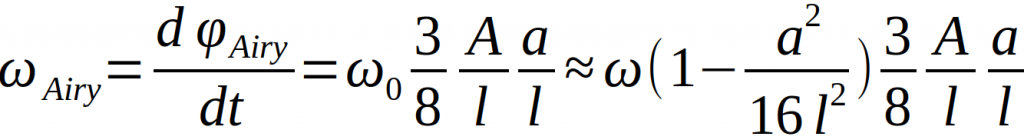
Da das Pendel frei um die z-Achse drehbar gelagert bzw. aufgehängt ist, führt zusätzlich noch der vom Breitengrad B des Standortes der Anlage abhängige sogenannte Coriolis-Effekt zu Drehungen. Hier sind Parallelen zu dem Foucault-Pendel zu erkennen, auf welches später noch eingegangen wird. Mit Einführung des Drehwinkels ϕ_Cor ergibt sich für die Winkelgeschwindigkeit aufgrund der Coriolis-Kraft

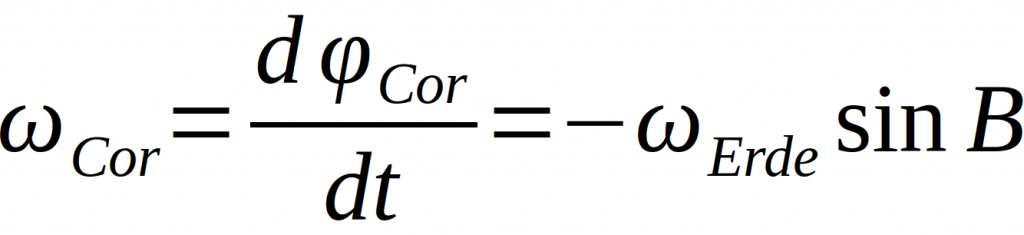
Die Winkelgeschwindigkeit der folgenden Drehbewegung der großen Bahnellipsen-Halbachse um A um den sogenannten Azimut-Winkel ϕ, resultierend aus dem Airy- und dem Coriolis-Effekt, ergibt sich nach

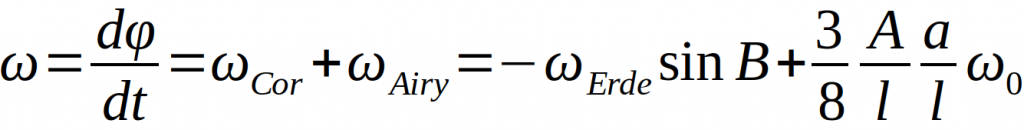
Der Wissenschaftler M. Allais nimmt an, dass der Airy-Effekt aufgrund von Dellenbildung in der Aufhängung des Parakonischen Pendels auftreten und versuchte durch Modifikation des Versuchsaufbaus und der verschiedenen Materialien diese Dellenbildung zu unterbinden bzw. zu minimieren. Dieser „neue“ Aufbau wird isotropes Pendel genannt. In mehreren Versuchsreihen zeigte sich, dass durch diese Änderungen deutlich höhere Winkelgeschwindigkeiten gemessen werden konnten, als erwartet. Dieser Effekt wird Allais-Effekt genannt [1].

M. Allais entwickelte folgende empirische Formel zur Beschreibung der Winkelgeschwindigkeit der Drehung der Bahnellipsen-Halbachse A bei parakonischen Pendeln

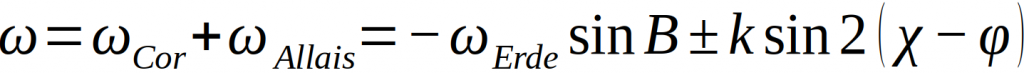
Wobei sich der sogenannte Allais-Effekt-Term wie folgt ergibt

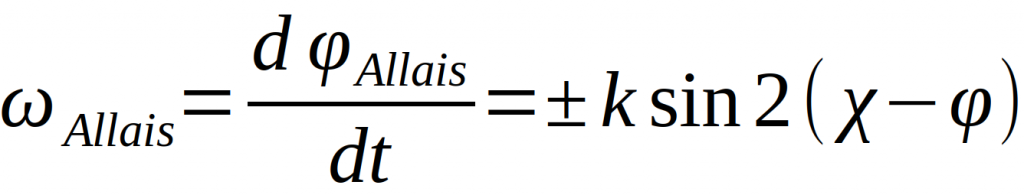
M. Allais hat den Parameter k nicht näher definiert, Χ beschreibt den Azimut des Effekts auf der Erdoberfläche. Laut Allais ist dieser Effekt ein durch anisotrope irdische, lunare und solare Gravitationsfelder bzw. Raumkrümmungen hervorgerufener modifizierter Airy-Effekt [1].

[1] Allais, Maurice: The “Allais Effect” and my experiments with the Paraconical Pendulum 1954 – 1960; NASA; 1999

[2] Göde-Stiftung: The Paraconical Pendulum reconsidered, (Link: https://goede-stiftung.org/the-paraconical-pendulum-reconsidered-2), aufgerufen am 07.05.2020

[3] Stöcker: Taschenbuch der Physik, Verlad Europa-Lehrmittel, 8. Auflage, 2018

Weiterführende Literatur:

[4] Savrov, L. A.: Paraconical pendulum as a detector of gravitational effects during solar eclipses (processing data and results); Measurement Techniques 38; 1995

[5] Allais, Maurice F. C.: Should the Laws of Gravitation Be Reconsidered? Part II – Experiments in Connection With the Abnormalities Noted in the Motion of the Paraconical Pendulum With an Anisotropic Support; École Nationale Supérieure des Mines, Paris; 10/1959

[6] Popescu, V. A.; Olenici, D.: A confirmation of the Allais and Jeverdan-Rusu-Antonescu effects during the solar eclipse from 22 September 2006, and the quantization of behaviour of pendulum; 2007

[7] Pugach, A. F.; Olenici, D.: Observations of Correlated Behavior of Two Light Torsion Balances and a Paraconical Pendulum in Separate Locations during the Solar Eclipse of January 26th, 2009; Advances in Astronomy, vol. 2012; 2012

Auf der Erde lässt sich künstliche Schwerelosigkeit (bzw. Gewichtslosigkeit) bisher nur  dadurch erreichen, dass man einen Körper frei fallen lässt. Dies wird in Parabelflügen mit  Flugzeugen oder in Falltürmen realisiert. Die erreichbare Dauer liegt im Bereich von wenigen  Sekunden (Fallturm) bis einigen Minuten (Parabelflug).

Bekannt für sogenannte “Gravitationsanomalien” sind Orte wie Roca di Papa in Italien oder  Karpacz Gorny in Polen. Erst durch präzise Messungen konnte geklärt werden, worum es bei diesen Phänomenen wirklich geht. Die naheliegendste Erklärung ist eine optische Täuschung, die einem vorgaukelt, dass es bergauf geht, obwohl es in Wirklichkeit bergab geht. Dass ein nahegelegener Berg die Richtung der Gravitation verändert, ist praktisch ausgeschlossen, aufgrund der viel zu geringen Masse im Verhältnis zur Erde.

Übertragen Gravitonen die Gravitationskraft?

Um diese Frage zu beantworten, sollte zunächst geklärt werden, was Gravitonen sind. Das Standardmodell der Physik umfasst 17 Teilchen, welche den Aufbau der Materie und die Grundkräfte, die zwischen Teilchen der Materie wechselwirken, erklären. Für eine der fundamentalen Wechselwirkungen, der Gravitation, konnte bisher kein sogenanntes Austauschboson zur Übertragung der Kräfte nachgewiesen werden. Dieses bis heute nicht nachgewiesene Teilchen wird „Graviton“ genannt. Das Graviton wird als masseloses Teilchen der Spin-Zahl 2 beschreiben. Andere schon bekannte Eichbosonen (Austauschteilchen) haben herkömmlicherweise die Spin-Zahl 1 [1].

Ähnlich wie bei Photonen wird erwartet, dass die Ruhemasse des Gravitons null ist, da die Gravitation, genauso wie elektromagnetische Wechselwirkungen, prinzipiell eine unendliche Reichweite besitzt. Außerdem wird vermutet, dass sich Gravitonen ebenfalls mit Lichtgeschwindigkeit bewegen. Wichtig ist, dass sie nicht mit den sogenannten unquantisierten Gravitationswellen verwechselt werden dürfen, denn diese folgen aus den Einsteinschen Feldgleichungen der Allgemeinen Relativitätstheorie, einer unquantisierten Theorie. Die Gravitonen sind Quanten und müssen somit mit quantenfeldtheoretischen Konzepten beschrieben werden [3].

Das Problem aus experimenteller Sicht ist die extreme Schwäche dieser gravitativen Kräfte. Um die Gravitonen dennoch aufspüren zu können, wurden immer empfindlichere Geräte entwickelt, wie z.B. LIGO, das Laser Interferometer Gravitational Wave Observatory. LIGO nutzt höchst sensible Interferometer, um auch kleinste Veränderungen im Ereignisraum aufzuspüren und so Gravitationswellen nachzuweisen. Denn sobald eine Gravitationswelle die hochkonzentrierten Laserstrahlen passiert, verändert sich der Ereignisraum und es kommt zu einer Phasenverschiebung der Teilwellen des Laserlichts und somit der Intensität des Lichts, was sich wiederrum messen lässt. Das Problem ist, dass selbst dieser Effekt schon extrem klein ist und die Sensibilität bei der Messung von Gravitonen noch deutlich verstärkt ist [2].

Es gibt eine Vielzahl von Theorien rund um die Gravitonen, z.B. die Annahme, dass Gravitonen nicht masselos sind, sondern dass es eine Obergrenze für die Gravitonenmasse geben müsste, oder dass sich die Gravitation in einem höherdimensionalen Raum, dem 3-Bran plus Extradimensionen, dem Bulk, ausbreiten kann. Letztere Theorie hätte die Konsequenz, dass Gravitonen, die in hochenergetischen Stößen (Teilchenbeschleunigern) entstehen, in Extradimensionen verschwinden und Energie forttragen könnten. Die verschiedenen Theorien werden unteranderem in Teilchenbeschleunigern versucht zu überprüfen, um letztlich vielleicht doch irgendwann Gravitonen zu entdecken [3], [4], [5], [6], [7], [8].

[1] Max-Planck-Institut für Physik: Gravitationstheorie: Auf den Spuren der Gravitationskraft (Link: https://www.mpp.mpg.de/forschung/aufbau-der-materie/gravitationstheorie/), aufgerufen am 25.06.2020

[2] Jogelakar, Ashutosh: Gravitonen: Entpuppt sich die Suche nach der Weltformel als Hirngespinst? (Link: https://www.spektrum.de/kolumne/entpuppt-sich-die-suche-nach-der-weltformel-als-hirngespinst/1193613), aufgerufen am 25.06.2020

[3] Lexikon der Astronomie: Graviton (Link: https://www.spektrum.de/lexikon/astronomie/graviton/158), aufgerufen am 25.06.2020

[4] Kostelecky, V. Alan; Samuel, Stuart: Photon and graviton masses in string theories; Phys. Rev. Lett. 66, 1811; 08.04.1991

[5] Van Dam, H.; Veltman, M.: On the mass of the graviton; General Relativity and Gravitation, 1972

[6] Corley, Steven; Lowe, David A.; Ramgoolam, Sanjaye: Einstein-Hilbert action on the brane for the bulk graviton; Journal of High Energy Physics, Volume 2001; 29.08.2001

[7] Davoudiasl, Hooman; Rizzo, Thomas G.: Bulk physics at a graviton factory; Physics Letters B, Volume 512; 12.07.2001

[8] Kanti, P.; Kodama, R. A.; Pappas, N.; Zhdenko, A.: Graviton emission in the bulk by a simply rotating black hole; Phys. Rev. D 80, 084016; 14.10.2009

Weiterführende Literatur:

[9] Adam, Z. R.: Evidence of gravitons as fused photons in four dimensions; 06/2009

[10] Bern, Z.; De Freitas, A.; Wong, H. L.: On the Coupling of Gravitons to Matter; 12/1999

[11] Boulanger, Nicolas; Damour, Thibault; Gualtieri, Leonardo; Henneaux, Marc: Inconsistency of interacting, multi-graviton theories; Nuclear Physics B, Volume 597; 12.03.2001

[12] Penrose, Roger: The nonlinear graviton; General Relativity and Graviton 7; 02/1976

[13] Kan, Nahomi; Shiraishi, Kiyoshi: Multi-graviton theory, a latticized dimension and the cosmological constant, Classical and Quantum Gravity, Volume 20, Number 23; 17.10.2003

[14] Becker, Katrin; Becker, Melanie; Polchinski, Joseph, Tseytlin, Arkady: Higher order graviton scattering in M(atrix) theory; Phys. Rev. D 56, R3174; 15.09.1997

Albert Einstein postulierte im Jahr 1916 die Existenz von Gravitationswellen, da sich diese Verzerrungen der vierdimensionalen Raumzeit aus seiner Allgemeinen Relativitätstheorie ergeben. Die Theorie besagt, dass zwei Massen nicht mehr wie von Newton beschrieben über die Schwerkraft in Wechselwirkung treten, sondern dass die Materie die Raumzeit in ihrer Umgebung verformt und beeinflusst. Das bedeutet, dass ein Körper, wenn er in die Nähe dieser Verformung gerät, abgelenkt wird und auf eine krumme Bahn gezwungen wird. Jedes Mal, wenn Materie in der Raumzeit den Bewegungszustand, also z.B. Geschwindigkeit oder Richtung ändert, entstehen Schwingungen, sogenannte Gravitationswellen. Je kompakter und massereicher die Objekte (Schwarze Löcher, Neutronensterne etc.) sind, desto stärker ist der Effekt ausgeprägt. Gravitationswellen breiten sich im Vakuum mit Lichtgeschwindigkeit aus, sind transversal und besitzen zwei Polarisationsfreiheitsgrade. Sie sind in der Lage, die Metrik der Raumzeit temporär zu beeinflussen und Massen senkrecht zu ihrer Ausbreitungsrichtung zu beschleunigen. Die Frequenz der Wellen liegt zwischen 10^-18 Hz bis 10⁴ Hz [1], [2], [3], [4].

Dadurch, dass die Wechselwirkung von Materie und Gravitationswellen extrem schwach ist, ist es schwer sie zu messen. Im September 2015 gelang es Physikern das erste Mal, Gravitationswellen mit Hilfe von Advanced-LIGO-Detektoren (Abk. für „Laser Interferometer Gravitational-Wave Observatory“) in den USA nachzuweisen. Diese Anlage besteht aus kilometerlangen Röhren, durch welche Laserstrahlen geleitet werden, um die Verzerrung des Raumes zwischen zwei Messpunkten zu ermitteln. Das gemessene Signal ging von zwei sich umkreisenden Schwarzen Löchern in einer Entfernung von 1,3 Milliarden Lichtjahren aus, die sich zunächst immer näherkamen und schließlich miteinander verschmolzen [1], [5], [6], [7].

[1] Welt der Physik: Gravitationswellen (Link: https://www.weltderphysik.de/gebiet/universum/gravitationswellen/), aufgerufen am 25.05.2020

[2] Spektrum der Wissenschaft, Heft 12/15: Warten auf die Welle, Felicitas Mokler

[3] Spektrum: Lexikon der Physik: Gravitationswellen (Link: https://www.spektrum.de/lexikon/physik/gravitationswellen/6101), aufgerufen am 25.05.2020

[4] Einstein, Albert: Die Grundlage der allgemeinen Relativitätstheorie, Annalen der Physik, Vierte Folge, Band 49

[5] DLR_next Was sind Gravitationswellen? (Link: https://www.dlr.de/next/desktopdefault.aspx/tabid-6568/10784_read-24345/), aufgerufen am 25.05.2020

[6] Abbott, B.P.; et. Al.: LIGO: The Laser Interferometer Gravitational Wave Observatory; Reports on Progress in Physics, 05/2009

[7] GEO600 Gravitational Wave Detector: Was ist GEO600? (Link: https://www.geo600.org/1219076/About-GEO600), aufgerufen am 27.08.2020

Weiterführende Literatur:

[8] Abbott, B.P.; et. Al.: Observation of Gravitational Waves from a Binary Black Hole Merger; Physical Review Letters; 02/2016

[9] Canfora, F.; Vilasi, G.: Spin-1 gravitational waves and their natural sources; Physics Letter B, 02/2004

[10] Freise, Andreas; Strain, Kenneth: Interferometer Techniques for Gravitational-Wave Detection; Living reviews in relativity, 02/2010

[11] Portilla, M.; Lapiedra, R.: Generation of high frequency gravitational waves; Physical Review D, 01/2001

[12] Sathyaprakash, B.S.; Schutz, Bernhard F.: Physics, Astrophysical and Cosmology with Gravitational Waves; Living Reviews in Relativity, 03/2009

Die Geschichte der Erforschung von Gravitationswellen beginnt mit ihrer Vorhersage Albert Einsteins im Rahmen seiner Allgemeinen Relativitätstheorie 1916 [1]. Er schaffte es, eine Theorie zu formulieren, die die Ausbreitung der Gravitation von Raumpunkt zu Raumpunkt beschreibt [2], [3]. Nach der theoretischen Erklärung der Gravitationswellen dauerte es jedoch noch viele Jahre, bis die wissenschaftliche Gemeinschaft von der Existenz dieser überzeugt war und insgesamt knapp 100 Jahre bis 2015 der erste direkte Nachweis erfolgte.

Der erste indirekte Nachweis von Gravitationswellen erfolge 1974 am sogenannten Hulse-Taylor-Pulsar von Joseph Taylor und Russel Hulse mithilfe des großen Radioteleskops am Arecibo-Observatorium in Puerto Rico entdeckt werden konnte [4]. Es handelt sich hier um einen Binärpulsar, der mit einem Begleitstern ein sogenanntes gravitativ gebundenes Doppelsternsystem bildet und sich etwa 21000 Lichtjahre entfernt befindet. Heute weiß man, dass es sich genauer um zwei Neutronensterne mit ähnlichen Massen von 1,44 und 1,39 Sonnenmassen handelt. Der schwerere Stern ist der Pulsar, welcher in periodischen Abständen von 59 ms elektromagnetische Pulse mit einer Frequenz von 1,4 GHz aussendet. Sie entstehen, wenn ein Stern ein stark gebündeltes, entgegen der Drehachse gekipptes Magnetfeld besitzt und sich mit dieser Periode um die eigene Achse. Es entsteht ein zeitlich veränderliches magnetisches Dipolfeld sowie eine elektromagnetische Strahlung, die gebündelt emittiert wird und dadurch einmal in 59 ms die Erde trifft. Durch den Doppler-Effekt konnte die Periode, mit der sich die Sterne umeinander bewegen auf 7,75 h bestimmt werden, allerdings bewegen sie sich nicht im Kreis umeinander, sondern auf präzidierenden Ellipsen hoher Exzentrizität von 0,6 um einen gemeinsamen Schwerpunkt. Diese Präzession der Ellipsen wurde schon im Rahmen der Allgemeinen Relativitätstheorie vorhergesagt. Im Fall des Hulse-Taylor-Pulsar beträgt sie 4,2 Grad pro Jahr, der 36000-fache Wert Merkurs [5].

Wird nun diesem Binärsystem ständig Energie durch emittierte Gravitationswellen entzogen, ändern sich die Bahnparameter (Halbachse, Periode, Exzentrizität, …) zeitlich korreliert, so dass die Gleichgewichtsbedingung zu jedem Zeitpunkt erfüllt ist. Mit Hilfe des dritten Kepler’schen Gesetzes und der vereinfachenden Annahme, dass die Massen beider Pulsare gleich sind und die Umlaufbahn kreisförmig ist, lässt sich die Änderungsrate der Periode vereinfacht wie folgt berechnen

Für den Fall von M=1,4 Sonnenmassen und der zuvor bestimmten Periodendauer von 7,75 h erhält man für die Änderungsrate . Da in dem Falle des Hulse-Taylor-Pulsars die Massen nicht gleich sind und die Bahnen nicht kreisförmig, muss der Wert korrigiert werden und ergibt sich schließlich zu , was bis auf eine Genauigkeit von 0,2 % mit dem beobachtenden Wert übereinstimmt.

Für diesen ersten indirekten Nachweis von Gravitationswellen und der Entdeckung des Pulsares PSR B1913+16 erhielten Hulse und Taylor 1993 den Nobelpreis [5] [6].

Für den direkten Nachweis von Gravitationswellen begann man in den siebziger Jahren mit Laserinterferometern zu arbeiten. Die Idee dieses Prinzips ist, dass Laserlicht von einer Quelle auf einen sogenannten Strahlteiler trifft, der zwei Teilstrahle erzeugt, die sich senkrecht voneinander wegbewegen, jeweils an Spiegeln reflektiert und zur Interferenz gebracht werden. Diese lässt sich wiederrum mit Hilfe eines Detektors nachweisen. Um eine ausreichende Genauigkeit zu erreichen, bewegt sich das Laserlicht in luftleeren Röhren. Wenn nun eine Gravitationswelle senkrecht auf diese Anordnung trifft, so werden die relativen Abstände zu den Spiegeln verändert und es kommt zu einer messbaren Verschiebung des Interferenzmusters. In der folgenden Abbildung ist ein schematischer Aufbau dargestellt [5].

Da die messbaren Effekte so klein und dabei sehr störanfällig (durch zum Beispiel seismische Effekte oder auch einfacher Straßenverkehr) sind, ist hierfür eine ausgeklügelte Technologie notwendig. Außerdem müssen, um die beschriebenen Störungen erkennen zu können, jeweils mindestens zwei Interferometer an unterschiedlichen Orten das gleiche Signal empfangen [5].

[1] Einstein, A.: Die Grundlage der allgemeinen Relativitätstheorie; Ann. D. Phys. 49; 1916

[2] Einstein, A.: Näherungsweise Integration der Feldgleichungen der Gravitation, Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften; Sitzung der physikalisch-mathematischen Klasse vom 22. Juni; 1916

[3] Einstein, A.: Über Gravitationswellen; Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften, Berlin; 31.01.1918

[4] Hulse, R. A.; Taylor, J. H.: Discovery of a Pulsar in a Binary System; Department of Physics and Astronomy, University of Massachusetts, Amherst; Tha Astrophysical Journal, 195, 15.01.1975

[5] Guilini, Domenico; Kiefer, Claus: Gravitationswellen; Einblicke in Theorie, Vorhersage, und Entdeckung; Springer Spektrum; 2017

[6] Weiss, Rainer: Nobel Lecture: LIGO and the discovery of gravitational waves; Rev. Mod. Phys. 90, 18.12.2018

Weiterführende Literatur:

[7] Thorne, Kip S.: Nobel Lecture: LIGO and gravitational waves III, Rev. Mod. Phys. 90, 040503, 18.12.2018

[8] Weber, J.: Detection and Generation of Gravitational Waves; Phys. Rev. 117, 306, 01.01.1960

[9] Barish, Barry C.; Weiss, Rainer: LIGO and the Detection of Gravitational Waves; Physics Today 52(10), 44; Oktober 1999

[10] Blair, David G.: The detection of gravitational waves; University of Western Australia; Cambride University Press; 1991

[11] Accadia, T.; et. Al.: Virgo: a laser interferometer to detect gravitational waves; Journal of Instrumentation, Volume. 7, March 2012

• Die frühen Anfänge der Gravitationsforschung gehen auf den griechischen Gelehrten Aristoteles (384 – 322 v. Chr.) zurück. Damals war das vorherrschende Weltbild das der ruhenden Erde im Zentrum, und um sie kreisten die Sonne, Mond und Planeten. Aristoteles versuchte damals schon die Bewegung fallender Körper zu beschreiben. Für ihn war der gerade Fallweg ein Beleg für die ruhende Erde [1]
• Einige Jahre später (100 – 160 n. Chr.) Erfolgte eine kleine Modifikation des Modells durch den alexandrinischen Gelehrten Clausius Ptolemäus. Sein Modell basiert ebenfalls auf der Geozentrizität und besagt, dass sich die Mittelpunkte der Kreisbahnen (z.B. Planeten oder Monde) ebenfalls auf Kreisen bewegen [1]
• Der erste, der systematisch und mathematisch Gravitation erforschte war Galileo Galilei (1564 – 1642). Er soll Fallexperimente am Schiefen Turm von Pisa durchgeführt haben, um seine Hypothesen zu überprüfen. Er konnte das kopernikanische, heliozentrische Weltbild bestätigen [1].
• Einen großen Durchbruch in der Gravitationsforschung erlangte Sir Isaac Newton (1643 – 1727). Er schrieb seine Theorie in „Philosophiae naturalis principia mathematica“ nieder [2].
• 1666 begann Newton mit dem Versuch, die (empirischen) Kepler‘schen Gesetze zu beweisen und physikalisch zu erklären. Das Ergebnis war schließlich 1687 seine Publikation „Principia“, indem unter Anderem zum ersten Mal die heute als Newtonsche Gesetze bekannten Gesetze erläutert werden: Das Trägheitsgesetz, das dynamische Grundgesetz und das Reaktionsprinzip. Weiter besagt Newtons Theorie, dass sich Gravitation instantan, also ohne Laufzeitverzögerung ausbreitet [1] [2].
• Albert Einstein (1879 – 1955) präsentierte im Jahr 1916 seine Allgemeine Relativitätstheorie, im Rahme dessen die Gravitation nicht als Kraft, sondern als geometrische Eigenschaft von Raum und Zeit beschrieben wird. Die ART wurde in zahlreichen Experimenten bestätigt [3].
• Eine alternative Gravitationstheorie sind solche mit Torsion, in denen der Torsions-Tensor, anders als bei der torsionsfreien Allgemeinen Relativitätstheorie, nicht verschwindet. Das Ergebnis ist eine deutlich kompliziertere Alternative zur Allgemeinen Relativitätstheorie mit einigen zusätzlichen Termen. Ein Beispiel ist zum Beispiel der sogenannte Fernparallelismus, der 1928 von Einstein als neue Gravitationstheorie mit ebendieser Torsion erfunden wurde. Schwerkraft ist nun keine Folge der Krümmung der Raumzeit mehr, sondern eine Folge der Verdrillung der Raumzeit. Gravitationsforscher konnten beweisen, dass der Fernparallelismus und die Allgemeine Relatitivätstheorie als gleichwertige Formulierungen angesehen werden können. Auch in der modernen Gravitationsforschung wird versucht, diese Theorien weiter zu entwickeln, um eventuell auf diesem Wege eine Theorie zu finden, die der Einsteinschen übergeordnet ist oder Querverbindungen zu z.B. Quantengravitationstheorien ergibt [1] [4].
• Die Skalar-Tensor-Theorien verfolgen den Ansatz, dass neben dem metrischen Tensor ein weiteres Skalares Feld vorliegt. Diesem Feld werden verschiedene Eigenschaften zugeschrieben, z.B. dass es in jedem Raumzeitpunkt konstant sein kann oder variieren kann. Außerdem koppelt es nur an den Krümmungsskalar (Ricci-Skalar), nicht an den metrischen Tensor. Es gibt unterschieldiche Varianten der Skalar-Tensor-Theorien, z.B. die Brans-Dicke-Theorie [1] [5] [6].
• Eine recht bekannte alternative Theorie ist die MOND-Theorie, die 1983 von dem Physiker Mordehai Milgrom aufgestellt wurde. Sie korrigiert das Newtonsche Gravitationsgesetz um einen weiteren Faktor, der von der Beschleunigung abhängt und ohne den Ansatz der Dunklen Materie unter Anderem das Rotationsverhalten von Spiralgalaxien erklären kann [7].
• Eine Ableitung der MOND Theorie ist TeVeS, die Tensor-Vektor-Skalar-Gravitationstheorie, die 2004 von Jacob D. Bekenstein aufgestellt wurde. Im Gegensatz zu den Skalar-Tensor-Theorien ist hier ein zusätzliches Vektorfeld vorhanden. Untersuchungen der letzten Jahre zeigen, dass diese Theorie gleichermaßen wie Einsteins Theorie Beobachtungen der modernen Kosmologie erklären kann [8] [1].
• Pseudo-Newtonsche Gravitation: Der Ansatz der Pseudo-Newtonschen Gravitation besteht aus einem 1980 von B. Paczynski und P. Wiita aufgestellten Modell, welches das Schwerefeld einer Punktmasse relativistisch mit der Schwarzschild-Lösung beschreibt. Es wird die Potentialformulierung statt der typischen Tensorschreibweise. Statt dem üblichen Newtonschen Potential wird das Paczynski-Wiita-Potential verwendet, welches mit dem Schwarzschildradius skaliert wird. Bis zu einem gewissen Grad können Gravitationseffekte um eine Punktmasse und nahe eines beispielhaften Schwarzen Loches beschrieben werden. Die Genauigkeit, mit der andere relativistische Effekte berechnet werden können, beträgt circa 10-20 % (wenn Radien außerhalb der sogenannten marginal stabilen Bahn, in diesem Fall sechs Gravitationsradien, betrachtet werden [9] [1].
• Gravitation mit Extradimensionen: Eine weitere Gruppe von Gravitationstheorien sind die Feldtheorien mit Extradimensionen, in welchen eine weitere Raum-, aber keine weitere Zeitdimension zugelassen wird. Allein die Gravitation wirkt auch in höheren Raumdimensionen, nicht aber die weiteren Naturkräfte. Ein Vorteil dieser Theorien ist es, dass das Hierarchieproblem der Physik erklärt werden kann. Der erste Vorschlag geht auf die Kaluza-Klein-Theorie zurück, die als fünfdimensionale Feldtheorie den Elektromagnetismus und die Allgemeine Relativitätstheorie vereinheitlichen sollte. Weitere bekannte Modelle sind zum Beispiel das ADD-Szenario, das DGP-Szenario, das Zyklische Universum und die Randall-Sundrum_Modelle [1]
• Die f(R)-Gravitation beschreibt eine Modifikation von Einsteins Allgemeiner Relativitätstheorie, allerdings werden hier nichtlineare Zusatzterme berücksichtigt, welche wiederum eine beliebige Abhängigkeit von dem Ricci-Skalar R besitzen können. Die Beschreibung der Gravitation in dieser Theorie wird über eine Feldgleichung bestimmt, die aus dem Wirkungsfunktional resultiert. Interessant sind diese f(R)-Theorien, da diese die Rolle der Dunklen Energie übernehmen könnte. Erfolgreiche Resultate zur Verifizierung dieser Theorien sind bisher noch nicht ausreichend vorhanden [10] [1].

[1] Spektrum: Lexikon der Astronomie: Gravitation; (Link: https://www.spektrum.de/lexikon/astronomie/gravitation/150)

[2] Newton, Sir Isaac: Philosophiae Naturalis Principia Mathematica; 1687

[3] Einstein, Albert: Die Grundlage der allgemeinen Relativitätstheorie; Ann. D. Phys. 49; 1916

[4] Einstein, A.: Zur Theorie der Räume mit Riemann-Metrik und Fernparallelismus; Sonderausgabe aus den Sitzungsberichten der Preussischen Akademie der Wissenschaften; Phys-Math. Klasse; 1930

[5] Bronnikov, K. A.: Scalar-Tensor Theory and Scalar Charge; State Board of Standards, USSR Ministerial Council, Moskau; 19.07.1972

[6] Wagoner, Robert V.: Scalar-Tensor Theory and Gravitational Waves; Phys. Rev. D. 1, 3209; 15.06.1970

[7] Milgrom, Mordehai: MOND: time for a change of mind? (08/2009)

[8] Bekenstein, Jacob D.: Tensor-vector-scalar modified gravity: from small scale to cosmology; Philosophical Transactions of the Royal Society A; Mathematical, Physical and Engineering Sciences; 28.12.2011

[9] Paczynsky, B.; Wiita, P. J.: Thick accretion disks and supercritical luminosities; Astronomy and Astrophysics, Vol. 500, p. 203-211; 08/1980

[10] Capozziello, S.; De Laurentis M.: Extended Theories of Gravity; Physics Reports 509: 167; 2011

Weiterführende Literatur

[11] Misner, C. W.; Thorne, K. S.; Wheeler, J. A.: Gravitation, Freeman San Francisco 1973

[12] Hawking, Stephen: Die Klassiker der Physik; Hamburg; 2004

[13] Stiefel, E.: Richtungsfelder und Fernparallelismus in n-dimensionalen Mannigfaltigkeiten; Commentarii Mathematici Helvetici 8, 305-353; 1935

[14] Bergmann, Peter G.: Comments on the Scalar-Tensor Theory; International Journal of Theoretical Physics, Vol. 1, 1968

[15] Fujii, Yasunori; Maeda, Kei-Ichi: The Scalar-Tensor Theory of Gravitation; Cambridge Monographs on Mathematical Physics; 2003

[16] Milgrom, Mordehai: New Physics at Low Accelerations (MOND): an Alternative to Dark Matter

[17] Milgrom, Mordehai: Dynamics with a non-standard inertia acceleration relation: an alternative to dark matter; Ann. Phys. 229, 1994 (Link: doi:10.1006/aphy.1994.1012), aufgerufen am 20.08.2020

[18] Skordis, Constantinos: The tensor-vector-scalar theory and its cosmology; Classical and Quantum Gravity, Volume 26, Number 14; 29.06.2009

[19] Abramowicz, M. A.: The Paczynski-Wiita potential. A step-by-step “derivation” – Commentary on: Paczynski B. and Wiita P. J.; 1980, A&A; 88, 23; (Link: https://www.aanda.org/articles/aa/full_html/2009/22/aa12155-09/aa12155-09.html)

[20] Hoyle, Fred; Narlikar, J. V.: A new theory of gravitation; Royal Society; 03.11.1964

Quantenphysik meets Relativitätstheorie?

Die Quantengravitation beschreibt eine Theorie, welche Einsteins Allgemeine Relativitätstheorie und die Quantentheorie konsistent zusammenführt, da sie sonst im Rahmen der bekannten physikalischen Grenzen nicht miteinander vereinbar sind. Es treten zwar erst in kleinen Abständen von 10^-33 cm Widersprüche auf, aber wenn es darum geht Vorgänge in schwarzen Löchern oder während des Urknalls zu erklären, müssen diese Diskrepanzen aufgelöst werden. Noch ist die Theorie der Quantengravitation nicht vollendet, es existieren jedoch verschiedene Ansätze [1].

Nach gegenwärtigen Erkenntnissen gehorcht die gesamte Physik der Quantentheorie, denn sowohl starke als auch elektroschwache Wechselwirkungen können hiermit erfolgreich beschrieben und erklärt werden. Das Problem tritt bei den gravitativen Wechselwirkungen auf, hinter denen die Allgemeine Relativitätstheorie steckt, denn diese können mit den vorherrschenden Quantentheorien nicht erklärt werden [1].

Grundsätzlich existieren zwei unterschiedliche Kategorien von Ansätzen für die Quantengravitation. Ein Ansatz besteht in der Annahme, dass Einsteins Theorie auch dann Bestand hat, wenn sie mit der Quantenmechanik konfrontiert wird. Es gilt also die Implikation, dass die Quantengravitation nicht mehr ist, als eine nichtstörungstheoretische Quantisierung der Einsteinschen Theorie und dass die Allgemeine Relativitätstheorie bei einer geeigneten Behandlung und Ergänzung durch das Standardmodell der Teilchenphysik auch bei kleinsten Abständen die physikalischen Freiheitsgrade korrekt beschreibt. Beispiele für Theorien mit diesem Ansatz sind die Schleifen- und Spinschaum-Quantengravitationstheorien [2], [3]. In diesen wird die Raumzeitmetrik durch Holonomien¹ und Flüsse als kanonische Variablen² beschrieben.

Bei dem zweiten Ansatz gilt die Allgemeine Relativitätstheorie nur als eine effektive Niedrigenergietheorie, die sich aus einer bisher noch unbekannten Planck-Skalentheorie ergibt, deren Freiheitsgrade sich wiederrum von denen der Allgemeinen Relativitätstheorie und der Quantenfeldtheorie unterscheiden. Beispiele für Theorien mit der Annahme, die Allgemeine Relativitätstheorie müsse durch eine andere, fundamentalere Theorie ersetzt werden sind die Supergravitations- und Superstringtheorie [4], [5], [6], [7].

Festzuhalten ist, dass sich bei beiden Ansätzen Probleme und offene Fragen ergeben, so kann die Stringtheorie zum Beispiel nicht formuliert werden, ohne sich auf einen bestimmten Raumzeithintergrund zu beziehen [4].

Schwierigkeiten bei der Konstruktion einer Quantengravitation bestehen auch darin, dass bisher keine Experimente zur Verfügung stehen, für die eine entsprechende Theorie relevant wäre. Generelle Anwendungsbereiche könnten zum Beispiel Quanteneffekte Schwarzer Löcher sein. Schwarze Löcher geben Strahlung thermischer Natur ab (Hawking-Effekt). Die Temperatur ist hier umgekehrt proportional zur Masse, mit dem Effekt, dass das Loch durch die Abstrahlung heißer wird und dabei an Masse verliert. Kommt diese Masse in den Bereich der sogenannten Planck-Masse, gelten die Annahmen aus der Ableitung des Hawking-Effekts nicht mehr, sodass nur eine Theorie der Quantengravitation vorhersagen könnte, wie das Endstadium bei der Verdampfung Schwarzer Löcher aussieht.

Vermutlich würde eine endgültige Theorie der Quantengravitation Effekte hervorbringen, die sich der Vorstellungskraft in der heutigen Zeit gänzlich entziehen.

[1] Lexikon der Physik: Quantengravitation (Link: https://www.spektrum.de/lexikon/physik/quantengravitation/11859), aufgerufen am 25.06.2020

[2] Bojowald, Martin: Zurück vor den Urknall; Die ganze Geschichte des Universums; 2010

[3] Ashtekar, Abhay; Rovelli, Carlo; Smolin, Lee: Gravitons and Loops, Phys. Rev. D 44, 15.09.1991

[4] Hermann, Nicolai: Quantengravitation und Vereinheitlichung; Max-Planck-Gesellschaft (Link: https://www.mpg.de/10847063/aei_jb_2016), aufgerufen am 26.06.2020

[5] Max-Planck-Institut für Gravitationsphysik (Albert-Einstein-Institut): Quantengravitation und Vereinheitlichte Theorien (Link: https://www.aei.mpg.de/176769/03_Quantum_Gravity_and_Unified_Theories), aufgerufen am 29.06.2020

[6] Wess, J.: Supergravitation; Naturwissenschaften 67, 10/1980

[7] Schwarz, John H.: Superstring theory; Physics Reports Volume 89, 09/1982

Weiterführende Literatur:

[8] Amelino-Camelia, G.; Lämmerzahl, C.; et. Al.: The Search for Quantum Gravity Signals, 01/2005

[9] Anderson, Edward: The Problem of Time in Quantum Gravity, Chapter 4 of „Classical and Quantum Gravity: Theory, Analysis and Applications“, 06/2012

[10] Hossenfelder, Sabine: Experimental Search for Quantum Gravity, „Classical and Quantum Gravity: Theory, Analysis and Applications“, Chapter 5, 10/2010

Ein kurzer Überblick über die Stringtheorie(n)

Die erste Stringtheorie wurde bereits um das Jahr 1970 aufgestellt, als Versuch, die Eigenschaften von Hadronen, also Teilchen aus Quarks und Gluonen, durch das Schwingungsverhalten eindimensionaler „Fäden“, sogenannten Strings, zu erklären. Mittlerweile existieren zahlreiche Varianten der Stringtheorien, wobei die Grundannahme stets die gleiche ist: Die Grundbausteine der Natur werden nicht mehr als punktförmige Teilchen angesehen, sondern verhalten sich wie eindimensionale Strings. Für die mathematische Konsistenz ergibt sich dadurch, dass sich das Universum in zehn Raumdimensionen ausdehnen muss, in welcher sich die supersymmetrischen Strings bewegen. Einige der Dimensionen lassen sich „aufrollen“, wodurch wir sie nicht direkt als tatsächlich existierende Raumrichtung wahrnehmen [1] [2] [3].

Generell existieren verschiedene Arten von Strings: Geschlossene und offene Strings. Die geschlossenen besitzen keine Endpunkte und haben so eine Topologie, die äquivalent zu der eines Kreises ist. Die offenen Strings haben jeweils zwei Enden und eine Topologie ähnlich zu der einer Strecke. Nicht alle Theorien besitzen offene Strings, aber alle haben geschlossene. Außerdem ist noch in Strings mit oder ohne Orientierung zu unterscheiden: Strings mit Orientierung besitzen stringinterne Pfeile, welche eine eindeutige Richtung bzw. Orientierung angeben [4].

Die Stringtheorien sind interessant, da sich dadurch die Möglichkeit ergibt, die bekannten theoretischen Unvereinbarkeiten bezüglich der Gravitation zwischen der Quantenphysik und der Allgemeinen Relativitätstheorie aufzulösen und somit die Antwort auf die Frage liefern zu können, wie sich die Gravitation bei geringen Abständen verhält. Interessant ist auch, dass sich aus Strings Objekte bilden lassen, die schwarzen Löchern ähnlich sind. Es bleibt jedoch die Frage, wie sich unsere gewohnte vierdimensionale Raumzeit mit der uns bekannten Physik aus diesen höherdimensionalen Theorien ableiten lässt [1] [3].

Die hauptsächliche Anwendung findet die Stringtheorie in der supersymmetrischen Version, welche die Symmetrie zwischen Bosonen und Fermionen beinhaltet, wobei es auch schon Weiterentwicklungen gibt, die sogenannten Brane-Theorien. Hier werden die Grundbausteine der Natur nicht als eindimensionale Strings, sondern als höherdimensionale Objekte, die Branes, angesehen [4].

Seit Mitte der 1980er Jahre definiert die Terminologie der Stringtheorien primär fünf verschiedene, zehndimensionale Stringtheorien:

• Typ I
• Typ IIA
• Typ IIB
• O-heterotisch oder auch SO(32)
• E-heterotisch oder auch E₈ x E₈

Typ I beschreibt sowohl offene als auch geschlossene, nicht orientierte Strings und elektrische Isolatoren. Offene Strings tragen elektrische Ladungen auf ihren Rändern mit Randbedingungen des Dirichlet-Typs und werden auch D-Brane genannt.

Die Typ IIA und Typ IIB Theorien beschreiben ausnahmslos geschlossene Strings als elektrische Isolatoren. Die Unterschiede zwischen den beiden Theorien liegen in der Orientierung der Strings, die es ausschließlich bei Typ IIB gibt und in der Eichsymmetrie. Während Typ IIB keine Eichsymmetrie besitzt, ist die von Typ IIA ist eine U(1)-Gruppe.

Die O- und E-heterotischen Theorien beschreiben ausschließlich geschlossene, orientierte und supraleitende Strings. Der Unterschied zwischen den beiden liegt ebenfalls in der Eichgruppe: Bei der O-heterotischen Theorie heißt diese SO(32) – bei der E-heterotischen E₈ x E₈. Beide Theorien bilden sich durch eine Kombination von Typ II und bosonischen Stringtheorien [2].

[1] Welt der Physik: Stringtheorie, (Link: https://www.weltderphysik.de/gebiet/teilchen/bausteine/jenseits-des-standardmodells/stringtheorie/), aufgerufen am 30.06.2020

[2] Spektrum: Stringtheorie, (Link: https://www.spektrum.de/thema/stringtheorie/1307212), aufgerufen am 30.06.2020

[3] Max-Planck-Institut: Stringtheorie, (Link: https://www.mpp.mpg.de/forschung/aufbau-der-materie/stringtheorie/), aufgerufen am 30.06.2020

[4] Physik Cosmos: Stringtheorie, (Link: https://physik.cosmos-indirekt.de/Physik-Schule/Stringtheorie), aufgerufen am 06.07.2020

Weiterführende Literatur:

[5] Maharana, Anshuman; Palti, Eran: Models of Particle Physics from Type IIB String Theory and F-Theory: A Review; International Journal of Modern Physics A Vol 28; 2013

[6] Karamanolis, Stratix: Die Stringtheorie: Phantom oder Realität?; 2008

[7] Rickles, Dean: A Brief History of String Theory: From Dual Models to M-Theory; 2014

[8] Blumenhagen, Ralph; Lüst, Dieter; Theisen, Stefan: Basic Concepts of String Theory; 2013

[9] Smolin, Lee: Die Zukunft der Physik: Probleme der Stringtheorie und wie es weitergeht; 2009

[10] Graña, Mariana; Triendl, Hagen: String Theory Compactifications; 2017

Mit Gravitation bezeichnet man die Eigenschaft von Massen, sich gegenseitig anzuziehen. Diese Anziehungskraft ist dabei gemäß dem Newtonsche Gravitationsgesetz von der Größe der Massen und von deren Abstand abhängig [1]. Sie nimmt quadratisch mit dem Abstand ab und benötigt zur korrekten Beschreibung noch eine Proportionalitätskonstante, die Gravitationskonstante G.

Newtonsches Gravitationsgesetz:

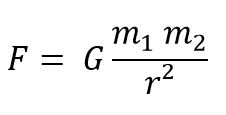
Der erste experimentelle Nachweis der Massenanziehung gelang Cavendish im Jahre 1798 mit einer Torsionswaage [2].

[1] Spektrum, Lexikon der Astronomie: Newtonsche Gravitation (Link: https://www.spektrum.de/lexikon/astronomie/newtonsche-gravitation/312)

[2] Harvard Natural Sciences Lecture Demonstrations: Cavendish Experiment (Link: https://sciencedemonstrations.fas.harvard.edu/presentations/cavendish-experiment)

Was ist das Urkilogramm?

Die Maßeinheit der Masse ist das Kilogramm [kg], eine der sieben Grundgrößen des internationalen Einheitensystems oder SI (frz. Système international d‘unités). 1889 wurde auf der ersten Generalkonferenz für Maß und Gewicht (CGPM) das sogenannte Urkilogramm, ein Platin-Iridium-Zylinder 39 mm hoch und 39 mm im Durchmesser und mit einer Masse von 1 kg, anerkannt und seitdem im Internationalen Büro für Maß und Gewicht (BIPM) in Sèvres bei Pari unter drei Glaskuppeln aufbewahrt [1], [2].

Das Problem mit dem über 130 Jahre alten Zylinder ist, dass er im Laufe der Jahre an Masse verlor. Als das Urkilogramm eingeführt wurde, wurden exakte Kopien angefertigt und in andere Länder transportiert, seitdem jedoch regelmäßig zusammengeführt und ihr Gewicht verglichen. Das Ergebnis war, dass die Massen sich zum Teil um ein halbes Mikrogramm pro Jahr unterscheiden – ein unhaltbarer Effekt. Im Detail kann dieser auch heute noch immer nicht verstanden werden wodurch es zu dem notwendigen Paradigmenwechsel kam [3].

Drei der sieben SI-Einheiten, nämlich Meter, Sekunde und Candela, können bereits seit Jahrzehnten rein aus Naturkonstanten hergeleitet werden und haben so keine begrenze Lebensdauer und verändern sich nicht mit der Zeit. Seit dem 20. Mai 2019 werden nun auch die anderen vier SI-Einheiten, das Kilogramm, das Ampere, das Kelvin und das Mol durch Naturkonstanten festgelegt und sind somit zeitlich ebenfalls nicht mehr veränderlich. Das Urkilogramm wurde abgelöst durch eine Beschreibung mit Hilfe des Planckschen Wirkungsquantums, bei der die Energiemenge einer Lichtwelle mit ihrer Frequenz verknüpft wird und somit stets denselben Wert hat [2].

[1] Stöcker; Taschenbuch der Physik; 2018; Europa Lehrmittel Verlag

[2] Gast, Robert; Spektrum News: Das Urkilogramm ist endgültig Geschichte (Link: https://www.spektrum.de/news/das-urkilogramm-ist-endgueltig-geschichte/1647288); aufgerufen am 04.05.2020

[3] Dr. Dr. Simon, Jens; Deutsche Physikalische Gesellschaft: PHYSIKonkret Nr. 34 September 2018 (Link: https://www.dpg-physik.de/veroeffentlichungen/publikationen/physikkonkret/pix/physik_konkret_34.pdf)

Weiterführende Literatur:

[4] Becker, Peter; Nicolaus, Arnold: Hat der Urkilogramm bald ausgedient?; 2008

[5] Unger, Wolfgang; Gross, Thomas; Lippitz, Andreas: Neues vom Urkilogramm; 2010

[6] Davis, R. S.: Possible new definitions of the kilogram; 2005

[7] Bich, W.: From the SI mass unit to multiples and submultiples: an overview; Metrologia Volume 40, Number 6; 27.11.2003

Seit dem 20. Mai 2019 wird die SI-Einheit der Masse nicht mehr über ein sogenanntes Urkilogramm definiert, sondern über die nicht veränderliche Planck’sche Konstante h. Grundlage ist, dass hier die Energiemenge einer Lichtquelle mit ihrer Frequenz verknüpft wird und somit stets denselben Wert hat. Über die Maßeinheit des Planck’schen Wirkungsquantums [kg m² s^-1] steht es in eindeutiger und direkter Beziehung zu Kilogramm, Meter und Sekunde [1], [2].

Um das Wirkungsquantum möglichst präzise zu bestimmen, wurde die sogenannte „Watt-Waage“ oder „Kibble-Waage“ des National Institute of Standards and Technology verwendet. Entwickelt hat diese Waage der Wissenschaftler Bryan Kibble im Jahr 1975 [3]. Sie besitzt einen Elektromagneten der auf einer Seite der Waage nach unten zieht und auf der anderen Seite ein Gewicht von bspw. einem Kilogramm. Nun wird der elektrische Strom durch den Magneten eingestellt, bis die Waage in perfekter Balance steht.

Der Strom durch den Elektromagneten wird sehr genau gemessen, wodurch die Planck’sche Konstante mit einer Genauigkeit von 0,000001% zu h=6,62607015 *10^-34 kg m² s^-1 bestimmt werden konnte [4], [5], [6].

[1] Gast, Robert; Spektrum News: Das Urkilogramm ist endgültig Geschichte (Link: https://www.spektrum.de/news/das-urkilogramm-ist-endgueltig-geschichte/1647288); aufgerufen am 04.05.2020

[2] Bureau International des Poids et Mesures: The International System of Units (SI) (Link: https://www.bipm.org/en/measurement-units/); aufgerufen am 14.08.2020

[3] Kibble, B.P.: A Measurement of the Gyromagnetic Ratio of the Proton by the Strong Field Method, National Physical Laboratory, 1976

[4] Ingenieur.de: Naturkonstanten definieren Basiseinheiten wie Kilogramm & Co. (Link: https://www.ingenieur.de/technik/fachbereiche/messtechnik/naturkonstanten-definieren-einheiten-wie-kilogramm-co/); aufgerufen am 04.05.2020

[5] Physik Cosmos: Ur-Kilogramm abgelöst – Neues Internationales Einheitensystem (SI) am 20.5.2019 in Kraft getreten (Link: https://physik.cosmos-indirekt.de/News/Ur-Kilogramm_abgel%C3%B6st_-_Neues_Internationales_Einheitensystem_(SI)_am_20.5.2019_in_Kraft_getreten.html), aufgerufen am 04.05.2020

[6] Bogers, Eric; Das Kilogramm ist tot – es lebe das Kilogramm! (Link: https://www.elektormagazine.de/news/das-kilogramm-ist-tot-es-lebe-das-kilogramm), Aufgerufen am 04.05.2020

Weiterführende Literatur:

[7] Göbel, Ernst: Wer gewinnt den Wettlauf um das Kilogramm?; Physikalische Blätter 57; 2001

[8] Jeckelmann, Beat; Beer, Walter: Hat das Urkilogramm ausgedient?; OFMET Info, 1998

Das Higgs-Teilchen entstammt ursprünglich einer Idee des Physikers Peter Higgs aus dem Jahr 1964. Die Idee war, dass ein Teilchen existiere, welches den anderen Materie-Teilchen Masse verleiht. Damals war man der Ansicht, dass Quarks, Elektronen und Neutrinos, ihrer mathematischen Definition nach, keine Masse besitzen, wodurch sie sich entgegen der Beobachtungen mit Lichtgeschwindigkeit bewegen würden – irgendetwas musste sie also bremsen. Nach Higgs Theorie sollen die Higgs-Teilchen ein feinmaschiges Netz bilden, in dem die Bestandteile der Materie hängen bleiben. Sie agieren wie ein Klebstoff, der die Elementarteilchen zusammenhält [1], [2], [3].

2013 haben Higgs und seine Partner den Nobelpreis für ihre Theorie bekommen, nachdem im Sommer 2012 im CERN erstmals Higgs Bosonen gefunden und nachgewiesen wurden [2], [4]. Durch den Fund der Higgs Bosonen am LHC wurde das Standardmodell der Teilchenphysik vervollständigt. Es besteht aus zwölf Elementarteilchen, auf welche die gesamte sichtbare Materie des Universums zurückgeführt werden kann. Higgs Bosonen sind elektrisch neutrale Austauschbosonen mit Spin 0 (Skalarfeld), deren Masse sehr hoch sein muss. Experimentell ließ sich die Massengrenze oberhalb von 114 GeV einordnen [2], [5].

Bis zur Entdeckung des Higgs-Teilchens im LHC war unklar, wie die Teilchen des Standardmodells zu ihrer Masse kommen. Die Masse von zusammengesetzten Teilchen wie zum Beispiel Protonen oder Neutronen konnte auf die starke Wechselwirkung zwischen ihren Bausteinen, also den Quarks, zurückgeführt werden. Denn durch die dynamischen Prozesse im Inneren wird nach Einsteins Formel Energie in Masse umgewandelt. Bei der Erklärung, wie die Elementarteilchen zu ihrer Masse kommen, versagte dieser Ansatz jedoch, da diese Teilchen keine innere Struktur besitzen, wodurch innerhalb der Teilchen keine Wechselwirkung zwischen verschiedenen Teilchen stattfindet und somit der Mechanismus mit Einsteins Formel E=mc² nicht mehr funktioniert [1], [5], [6].

Neben dem Problem der Massen ergab sich ein weiteres Problem: Bei dem Versuch, die Masse von Elementarteilchen in das Standardmodell zu integrieren traten unter anderem Wahrscheinlichkeiten von über hundert Prozent auf und es kam zu gravierenden inneren Widersprüchen. In der Vergangenheit wurde dieses Problem, sofern es auftrat, gelöst, indem neue Teilchen eingeführt wurden. In diesem Fall musste jedoch nicht nur ein neues Teilchen eingeführt werden, sondern ein neues Prinzip – den Higgs-Mechanismus.

Unabhängig voneinander entwickelten Francois Englert, Robert Brout und Peter Higgs den sogenannten Higgs-Mechanismus. Bei den folgenden Veröffentlichungen beleuchteten sie jeweils unterschiedliche Aspekte jedoch mit dem gleichen Grundgedanken: Die Elementarteilchen selbst besitzen die Masse Eigenschaft nicht [1], [6]. Der Begriff der Masse wurde umdefiniert und es wurde ein Feld postuliert, welches den gesamten Raum erfüllt und mit welchem die massebehafteten Elementarteilchen wiederum in Wechselwirkung treten und abgebremst werden. Der Higgs-Mechanismus beschreibt also, dass das Higgs-Feld, welches sich unendlich im Raum erstreckt, Teilchen mit Masse ausstattet und somit die spontane Symmetriebrechung bewirkt. Die Berechnungen von Englert, Brout und Higgs ergaben außerdem, dass die Einführung des Higgs-Feldes auch mit der Einführung eines neuen Elementarteilchens einher geht: das Higgs-Boson. Das Higgs-Boson koppelt sich an alle Teilchen und kann mit jedem wechselwirken, wobei die Stärke der Kopplung proportional zur Masse des Teilchens ist. Je mehr Masse dieses Teilchen hat, desto leichter kann es außerdem das Higgsfeld in Schwingungen versetzen [2].

Dank jahrelanger Messungen im LHC und Abgleich gesammelter Daten konnte die Masse des Higgs-Teilchens auf zwischen 114 und 180 Gigaelektronenvolt geteilt durch c² beschränkt werden. Da es einige Jahre dauerte, bis die Theorie 2012 wirklich bestätigt werden konnte und Higgs-Bosone nachgewiesen werden konnte, kamen mit der Zeit neue Theorien auf, welche einen alternativen Mechanismus oder einen modifizierten Higgs-Mechanismus beschrieben. Die Kritik der Theoretiker lag unter anderem darin, dass das Higgs-Teilchen einen ungewöhnlichen und unüblichen Eigendrehimpuls von Null hat und außerdem ausschließlich das Problem der Masse löst, wodurch der Mechanismus teils als „Hilfskonstruktion“ angesehen wurde [6].

Am 4.07.2012 wurde schließlich am LHC nach Billionen von gemessenen Daten verkündet, dass ein neues Teilchen nachgewiesen werden konnte, bei welchem Produktionsweise, Zerfall, Eigendrehimpuls und Masse so ausfallen, wie erwartet wurde [6].

Es gibt auch heute noch einige unbeantwortete Fragen, wie zum Beispiel ob das Higgs-Teilchen sich auch an sich selbst koppelt, um sich selbst Masse zu verleihen und ob derselbe Mechanismus auch für Kräfteteilchen gilt. Um diese Fragen beantworten zu können wird allerdings fortgeschrittene und verbesserte Technik, also bessere Detektoren und feinere Analysemethoden, benötigt, wenn nicht sogar ein neuer (Linear-)Beschleuniger [6].

Ein anderes Problem bietet außerdem die Gravitation – denn wenn diese hinzugezogen wird bricht das Standardmodell zusammen, da die Gravitation nicht Teil des Modells ist. Es müssen interne Korrekturen vorgenommen werden, wodurch das Modell zwar konsistent bleibt, jedoch weit entfernt von einer einfachen oder ästhetischen Theorie ist [6].

[1] Welt der Physik: Das Higgs-Teilchen, (Link: https://www.weltderphysik.de/gebiet/teilchen/bausteine/higgs/), aufgerufen am 15.07.2020

[2] Lexikon der Astronomie: Higgs-Teilchen, (Link: https://www.spektrum.de/lexikon/astronomie/higgs-teilchen/176), aufgerufen am 15.07.2020

[3] Higgs, Peter W.: Broken Symmetries and the Masses of Gauge Bosons, Tait Institute of Mathematical Physics, University of Edinburgh, 31.08.1964

[4] MLA style: The Nobel Prize in Physics 2013, (Link: https://www.nobelprize.org/prizes/physics/2013/summary/), aufgerufen am 16.10.2020

[5] Krause, Michael: CERN – How We Found the Higgs Boson, 08/2014

[6] Pollmann, Maike: Der Higgs-Mechanismus – von einer Idee zum Nobelpreis, (Link: https://www.weltderphysik.de/gebiet/teilchen/bausteine/higgs/higgs-mechanismus/) 07.07.2014, aufgerufen am 29.10.2020

Weiterführende Literatur:

[7] Barth, A.; Marx, W.; Bornmann, L.; Mutz, R.: On the origins and the historical roots of the Higgs boson research form a bibliometric perspective; The European Physical Journal Plus 129, Article No. 111, 06.06.2014

[8] Cho, Adrian: Higgs Boson Makes Its Debut After Decades-Long Search; Science Vol. 337, Issue 6091; 13.07.2012

[9] Dittmar, M.; Dreiner, H.: How to find a Higgs boson with a mass between 155 and 180 GeV at the CERN LHC, Phys. Rev. D 55, 167; 01.01.1997

[10] Duhrssen, M.; Heinemeyer, S.; et. Al.: Extracting Higgs boson couplings from CERN LHC data; Phys. Rev. D 70, 113009; 10.12.2004

Im 19. Jahrhundert wurde postuliert, dass sich elektromagnetische Wellen, wie alle anderen Wellen, in einem jeweils geeigneten Trägermedium, dem Äther, ausbreiten. Die Konsequenz war zwangsläufig, dass sich dieser Äther das gesamte Universum sowie das Innere der Materie erfüllen muss. Die wesentliche Eigenschaft dieses Äthers ist es, die in der Naturbeschreibung auftretenden Fernkräfte auf Nahwirkungskräfte zurückzuführen. In der Newtonschen Gravitationstheorie gelten Gravitationskräfte als solche Fernkräfte, die durch die Theorie eines Äthers direkt auf sogenannte Nahwirkungskräfte zurückgeführt werden konnten. Die Hypothese lautete, dass der Äther durch seine elastische Deformation Kräfte übertragen würde [1], [2].

Der Äther musste außerdem eine sehr geringe Dichte besitzen, gleichzeitig aber hochelastisch sein. Da der Äther das gesamte Universum erfüllen muss, also allgegenwärtig ist, würde er ein absolut ruhendes System definieren, dasjenige, indem er selbst ruht. Dadurch müsste er sich durch optische, interferometrische Experimente nachweisen lassen [3].

Die Geschwindigkeit von Wellen wird generell relativ zum Medium, in dem sie sich bewegen, gemessen, da sie von den Eigenschaften dieses Mediums abhängt. In Rahmen der Maxwellschen Elektrodynamik treten Unterschiede der Ausbreitung von elektromagnetischen Wellen in verschiedenen Bezugssystemen auf. Um diese Unterschiede erklären zu können, schien die Existenz eines sogenannten Lichtäthers mit Festkörpereigenschaften, welcher ausschließlich die Ausbreitung transversaler Wellen erlaubt, notwendig zu sein. Die Idee war es nun, die Geschwindigkeit der elektromagnetischen Wellen relativ zum Äther zu messen. Das Ergebnis war, dass der Äther selbst der Sitz der elektromagnetischen Felder sein müsse. Außer dem generellen Besitzen eines Bewegungszustandes, konnte dem Äther keine einzige mechanische Eigenschaft widerspruchsfrei zugeschrieben werden. Experimente wie z.B. das Michelson-Morley-Experiment oder der Trouton-Noble-Versuch ergaben, dass es nicht möglich ist, dem Äther eine Geschwindigkeit zuzuschreiben, auch nicht die Geschwindigkeit Null [2], [4], [5].

Anfang des 20. Jahrhunderts, vor allem durch die Spezielle Relativitätstheorie, verlor die Ätherhypothese immer mehr an physikalischer Bedeutung. Für die moderne Physik werden die im Rahmen der Ätherhypothese angeführten Fernkräfte durch die Verwendung des Feldbegriffs vermieden [2].

[1] Tipler, Paul; Llewellyn, Ralph: Moderne Physik, Oldenbourg, 2010

[2] Spektrum: Lexikon der Physik: Äther, (Link: https://www.spektrum.de/lexikon/physik/aether/854) aufgerufen am 07.05.2020

[3] Meschede, Dieter: Gerthsen Physik; Springer Verlag; 2006

[4] Michelson, A.A:; v. Laue, M.: Die Relativbewegung der Erde gegen den Lichtäther, 1931, (Link: https://doi.org/10.1007/BF01528662)

[5] Trouton, F.T.; Noble, H.R.: The mechanical forces acting on a charged electric condenser moving through space, 01.1904, (Link: https://royalsocietypublishing.org/doi/abs/10.1098/rsta.1904.0005 )

Weiterführende Literatur:

[6] Swenson, Loyd S.; Michelson, Albert Abraham; et. Al.: The ethereal aether: A history of the Michelson-Morsel-Miller aether-drift experiments

Die Spezielle Relativitätstheorie wurde 1905 von Albert Einstein im Artikel „Zur Elektrodynamik bewegter Körper“ veröffentlicht und später im Jahr 1915 in Spezielle Relativitätstheorie umbenannt. Sie war der erste Schritt einer fundamentalen Theorie [1], [2], [3].

Kurz Zusammengefasst ist die Spezielle Relativitätstheorie die Theorie der hohen Geschwindigkeiten und verschiedenen Beobachtern, die einen Vorgang in der Natur betrachten. Sie beschreibt die Transformation einzelner physikalischer Gesetze beim Wechsel des Bezugssystems. Diese Effekte werden besonders relevant, wenn die relative Geschwindigkeit zwischen den betrachteten Bezugssystemen vergleichbar mit der Lichtgeschwindigkeit im Vakuum wird [1], [7], [8], [9].

1881 und 1887 führten Michelson und Morley Experimente zum Nachweis des sogenannten Lichtäthers durch. In einer Anordnung von Lichtstrahlen sollte demnach die Mitbewegung des Lichtäthers und somit der Lichtwellen auf einem Interferometerarm nachgewiesen werden. Die Annahme war, dass sich das Interferenzmuster verändern würde, doch es war keiner Interferenzverschiebung beobachtbar [4]. Einstein erklärte diese Beobachtung mit der These, es gäbe keinen Weltäther und keinen Lichtäther und die Lichtgeschwindigkeit sei in allen Bezugssystemen konstant. Das erste Postulat der Speziellen Relativitätstheorie beschreibt also die Konstanz der Lichtgeschwindigkeit. Das zweite Postulat des Relativitätsprinzips beschreibt, dass physikalische Gesetze und Messungen in allen zueinander gleichförmig geradlinig bewegten Systemen gleich seien [2], [5], [6], [8].

Im Folgenden werden von Einstein sogenannte Inertialsysteme eingeführt, also Bezugssysteme von Objekten, die sich mit konstanter Geschwindigkeit relativ zueinander bewegen, während in allen Systemen dieselben physikalischen Gesetze gelten. Die Lorentz-Transformation sorgt dabei für die Konstanz der Lichtgeschwindigkeit beim Übergang von Inertialsystemen – Wege und Zeiten ändern sich hingegen bei der Anwendung der Transformation [2], [5].

Nach Einstein sind Raum und Zeit relativ und unmittelbar miteinander verbunden mit der Folgerung, dass Ereignisse nur gleichzeitig sind, wenn sie zu einem festen Zeitpunkt am selben Ort stattfinden [2], [3], [5], [6], [8].

Das Ergebnis der Speziellen Relativitätstheorie ist außerdem, dass mathematisch gesehen Zeitreisen in die Zukunft oder die Vergangenheit möglich sind; technisch gesehen eher nicht, da es physikalisch nur möglich sein kann, in die Zukunft zu reisen, während Reisen in die Vergangenheit dem Kausalitätsprinzip widerspricht.

Sobald Gravitationskräfte im Spiel sind, genügt die Spezielle Relativitätstheorie nicht mehr, da sie keinerlei Beschreibung der Gravitation enthält – hier wird die Allgemeine Relativitätstheorie benötigt [2].

[1] Lexikon der Astronomie: Spezielle Relativitätstheorie, Spektrum (Link: https://www.spektrum.de/lexikon/astronomie/spezielle-relativitaetstheorie/444), aufgerufen am 13.08.2020

[2] Sonne, Bernd: Spezielle Relativitätstheorie für jedermann – Ohne höhere Mathematik: Grundlagen und Anwendungen verständlich formuliert, Springer Spektrum, 2. Auflage, 2020

[3] Einstein, A.: Zur Elektrodynamik bewegter Körper; Das Relativitätsprinzip

[4] Michelson, Albert A.; Morley, Edward W.: On the Relative Motion of the Earth and of the Luminiferous Ether; Sidereal Messenger vol. 6; 10/1887

[5] Einstein, A.; Lorentz, H. A.; Weyl, H.; Minkowski, H.: The Principle of Relativity – A Collection of Original Memoirs on the Special and General Theory of Relativity; 2013

[6] Einstein, Albert: Äther und Relativitäts-Theorie; Rede gehalten am 05.05.1920 an der Reichs-Universität zu Leiden

[7] French, A. P.: Die spezielle Relativitätstheorie – M.I.T. Einführungskurs Physik, Vieweg + Teubner Verlag, Wiesbaden, 1986

[8] Einstein, A.: Die Grundlage der allgemeinen Relativitätstheorie, Ann. D. Phys. 49; 1916

[9] Woodhouse, Nicholas: Spezielle Relativitätstheorie; Springer Verlag; 2016

Weiterführende Literatur:

[10] Einstein, Albert; Übersetzt von Ono, Yoshimasa A.: How I created the theory of relativity; 1922

[11] Schlick, Moritz: Texte zu Einsteins Relativitätstheorie; 2019

[12] Manzel, Peter-Paul: Relativitätstheorie; 2005

[13] Rindler, Wolfgang: Relativitätstheorie: speziell, allgemein und kosmologisch; 2016

Das Äquivalenzprinzip, auch Einstein‘sches Äquivalenzprinzip genannt, gilt als die der Allgemeinen Relativitätstheorie zugrunde liegende Hypothese. Sie sagt aus, dass ein homogenes Gravitationsfeld einem gleichmäßig beschleunigten Bezugssystem äquivalent ist. Anders ausgedrückt bedeutet das, dass die schwere und die träge Masse eines Körpers zwei äquivalente Größen sind [1] [2] [3] [4].

Anschaulich betrachtet kann ein Beobachter in einem abgeschlossenen System (Kasten) nicht unterscheiden, ob sich dieser Kasten auf der Oberfläche einer Masse und somit in dessen Gravitationsfeld befindet oder ob er gleichmäßig durch eine konstant wirkende Kraft ohne Gravitationsfeld im freien Raum beschleunigt wird. Einstein erkannte 1907 dieses Grundprinzip einer Theorie der Gravitation, welches ihn schließlich zur Allgemeinen Relativitätstheorie führte [5] [6].

Es existieren zwei Formen: das schwache und das starke Äquivalenzprinzip. Das schwache Äquivalenzprinzip sagt aus, dass von allen Eigenschaften eines Körpers die Masse (=Maß der Trägheit) bestimmt, welche Schwerkraft in einem gegebenen homogenen Gravitationsfeld auf ihn wirkt, wodurch Eigenschaften wie die Größe, Form oder chemische Zusammensetzung keinerlei Einfluss darauf haben [7].

Beim starken Äquivalenzprinzip gilt, dass Gravitations- und Trägheitskräfte auf kleinen Abstands- und Zeitskalen in einem Sinn äquivalent sind, indem sie an ihren Wirkungen nicht unterschieden werden können, weder mechanisch noch durch andere Beobachtungen [7].

Es gilt, dass die Massen in der Form

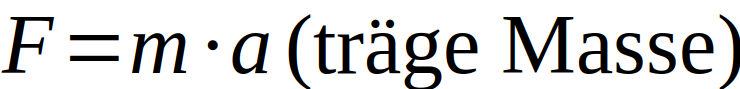
und

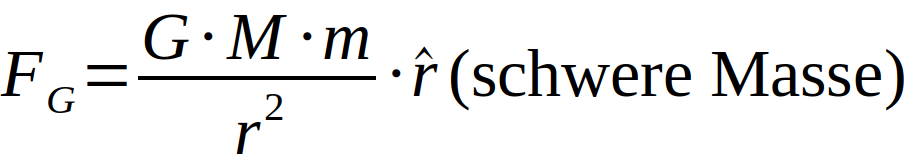
identisch sind [2].

Aus dem starken Äquivalenzprinzip folgt das schwache – ob diese Beziehung auch umgekehrt gilt ist Gegenstand aktueller Forschung und noch nicht geklärt.

Das schwache Prinzip konnte bereits durch diverse Experimente mit relativer Genauigkeit von bis zu 10^-13 bestätigt werden, sodass

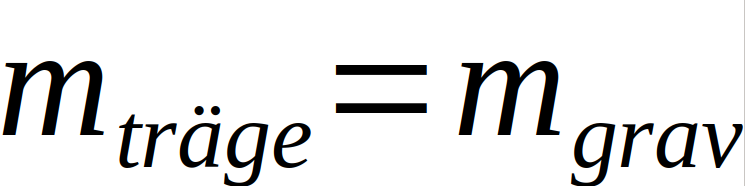
mit dieser Genauigkeit gilt. Die Folgerung des Prinzips ist also, dass es keine absolute Beschleunigung gibt und geben kann, sie ist, wie die Geschwindigkeit auch, immer relativ [2].

Der Physiker Eötvös führte bereits Ende des 19. Jahrhunderts Experimente mit einer Torsionswaage durch. Er wollte überprüfen, ob Körper aus unterschiedlichen Materialien in voneinander abweichende Richtungen fallen und somit das Verhältnis von schwerer und träger Masse bei den Messobjekten überprüfen. Solche Messungen zur Äquivalenz werden quantitativ über den sogenannten Eötvös-Faktor η beschrieben [8]:

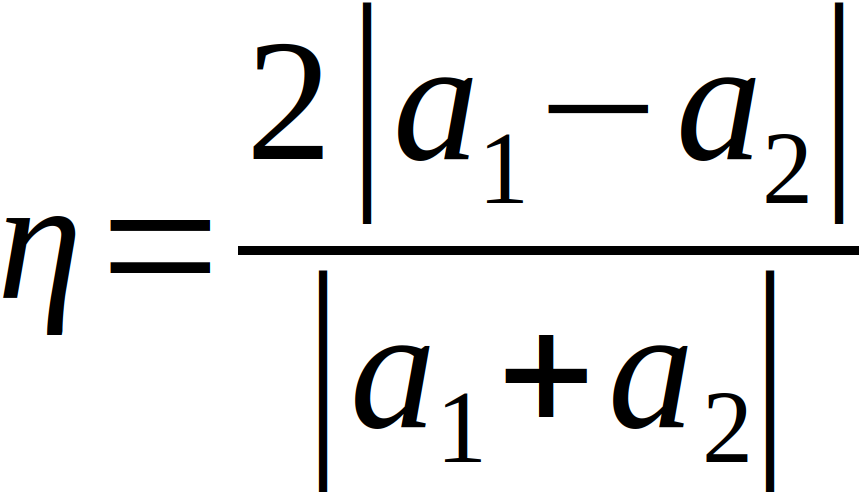
Mit a₁ und a₂ als gemessene Beschleunigungen der unterschiedlichen Testkörper [7] [9].

Die Torsionspendelversuche von Eötvös konnten die Grenze η auf weniger als 10^-9 begrenzen. Mittlerweile hat die Eöt-Wash Gruppe der University of Washington in Seattle den Parameter η mit einer Materialkombination aus Beryllium und Titan im Gravitationsfeld der Erde bis auf eine Genauigkeit von 10^-13 begrenzen können, das heißt, bis auf diese verbliebene Messungenauigkeit gilt dieser Teil des Äquivalenzprinzips [9] [10].

Schärfere Obergrenzen von η können beispielsweise durch satellitengestützte Experimente erreicht werden. In Frage kommen z.B. die STEP-Mission, Gravity Probe A oder auch MICROSCOPE [11] [12]. Die Idee dieser Experimente ist die Messung der relativen Beschleunigungen von im Orbit befindlichen, frei fallenden Testkörpern unterschiedlicher chemischer Zusammensetzung. Die zu erwartende Genauigkeit beträgt weniger als 10^-15 bei MICROSCOPE und sogar < 10^-18 bei STEP [7].

[1] Lexikon der Physik: Äquivalenzprinzip, (Link: https://www.spektrum.de/lexikon/physik/aequivalenzprinzip/712), aufgerufen am 29.06.2020

[2] Tipler, Paul; Llewellyn, Ralph: Moderne Physik, Oldenbourg Verlag

[3] Pössel, Markus: Kabine, Schwerkraft und Rakete: Das Äquivalenzprinzip; Einstein online (Link: https://www.einstein-online.info/spotlight/aequivalenzprinzip/), aufgerufen am 14.08.2020

[4] Hagedorn, Daniel; Selig, Hanns: MICROSCOPE: Äquivalenzprinzip im Weltraumtest, (Link: https://www.weltderphysik.de/gebiet/universum/teleskope-und-satelliten/microscope/), aufgerufen am 18.08.2020

[5] Lexikon der Astronomie: Äquivalenzprinzip, (Link: https://www.spektrum.de/lexikon/astronomie/aequivalenzprinzip/21), aufgerufen am 29.06.2020

[6] Einstein, Albert: Die Grundlage der allgemeinen Relativitätstheorie; Annalen der Physik, Vierte Folge, Band 49

[7] Äquivalenzprinzip (Physik), Physik Cosmos, (Link: https://physik.cosmos-indirekt.de/Physik-Schule/%C3%84quivalenzprinzip_(Physik)), aufgerufen am 29.06.2020

[8] Eötvös, Roland: Über die Anziehung der Erde auf verschiedene Substanzen; Akadémiai Értesíto, 02/1890

[9] Guilini, Domenico: Einstein im Quantentest, Spektrum der Wissenschaft 10/13 – Oktober 2013

[10] The Eöt-Wash Group: Laboratory Tests of Gravitational and Sub-Gravitational Physics; (Link: https://www.npl.washington.edu/eotwash), aufgerufen am 18.08.2020

[11] Space Microscope to test universality of freefall, The European Space Agency, 2016; (Link: http://m.esa.int/Our_Activities/Space_Science/Space_Microscope_to_test_universality_of_freefall), aufgerufen am 18.08.2020

[12] Bergé, Joel; Rodrigues, Manuel; Touboul, Pierre: Status of MICROSCOPE, a mission to the test the Equivalence Principle in Space

Weiterführende Literatur:

[13] Han, Feng-Tian; Wu, Qui-Ping; Zhou, Ze-Bing; et. Al.: Proposed Space Test of the New Equivalence Principle with Rotating Extended Bodies

[14] Wagner, T. A.; Schlamminger, S.; Gundlach, J. H.; Adelberger, E. G.: Torsion-balance tests of the weak equivalence principle

[15] Eötvös, Roland; Pekár Desiderius; Fekete, Eugen: Beiträge zum Gesetze der Proportionalität von Trägheit und Gravität

[16] Fischbach, Ephraim: Reanalysis of the Eötvös Experiment

Albert Einstein stellte seine Allgemeine Relativitätstheorie zwischen 1907 und 1916 auf. Sie gilt heute als klassische Theorie der Gravitation. Ausgehend von der Beschreibung von Trägheitskräften in der Speziellen Relativitätstheorie, dem Machschen Prinzip und dem Äquivalenzprinzip erkannte Einstein, dass die Gravitation, wie wir sie kennen, als Krümmung der Raumzeit manifestiert wird. Die Newtonsche Gravitationstheorie ist hier als nichtrelativistischer Grenzfall enthalten und obwohl sich die Vorhersagen der ART nur minimal von denen Newtons unterscheiden, wurde sie bisher von allen durchgeführten Experimenten bestätigt. Vorhersagen der ART waren unter anderem Schwarze Löcher und Gravitationswellen – beide wurden bisher indirekt beobachtet [1], [2], [3].

Ursprünglich resultierte die Theorie aus dem Versuch Einsteins, die spezielle Rolle der sogenannten Inertialsysteme aus der Relativitätstheorie zu eliminieren, um allgemeine, beliebig beschleunigte und rotierende Bezugssysteme gleichwertig zu erlauben. Trägheitskräfte lassen sich in inertialen Bezugssystemen lokal nicht von den Gravitationskräften unterscheiden, wodurch die Allgemeine Relativitätstheorie als eine Theorie der gravitativen Wechselwirkung gilt. Der Widerstand gegen eine Änderung der Geschwindigkeit (Trägheit) ist somit identisch mit der Ladung der Gravitation. Nimmt man die Erkenntnisse der speziellen Relativitätstheorie hinzu, nämlich dass Ort und Zeit und damit auch der Quotient, die Geschwindigkeit, zusammen eine vierdimensionale Raumzeit aufspannen und somit geometrische Größen darstellen, ergibt sich die Erkenntnis, dass Schwerkraft und Masse geometrische Größen sein müssen [1], [3].

Da außerdem die Äquivalenz von Masse und Energie gilt und wie zuvor erläutert Gravitation, Schwerkraft und Massenanziehung Krümmung der Raumzeit ist, krümmt jede Energieansammlung dementsprechend die Raumzeit. Für einen wirklich messbaren Effekt muss jedoch eine große Menge Energie in Raum und Zeit konzentriert werden.

Laut Einsteins Theorie breitet sich das Gravitationsfeld, genau wie auch das elektromagnetische Feld, wellenförmig und mit Lichtgeschwindigkeit aus. 2015 konnten diese Gravitationswellen erstmals direkt nachgewiesen werden [1], [4].

Schwarze Löcher, eine Vorhersage der ART, vereinen eine so große Masse bzw. Energie in sich, dass sie sowohl eine messbare Krümmung der Raumzeit bewirken, als auch sie so extrem krümmen, dass auch kein Licht mehr entkommen kann [1], [2].

Um die Feldgleichungen für seine Allgemeine Relativitätstheorie zu finden orientierte sich Einstein am Prinzip der allgemeinen Kovarianz, um die Formulierung der physikalischen Gesetze unabhängig vom Bezugssystem zu erhalten. Die mathematische Konsequenz war die Formulierung in tensoriellen Größen. Die Feldgleichungen bestimmen die Geometrie der Raumzeit in Abhängigkeit davon, wie sie bei bestimmter Energie- und Masseverteilung gekrümmt ist. Die Einstein-Gleichungen lauten

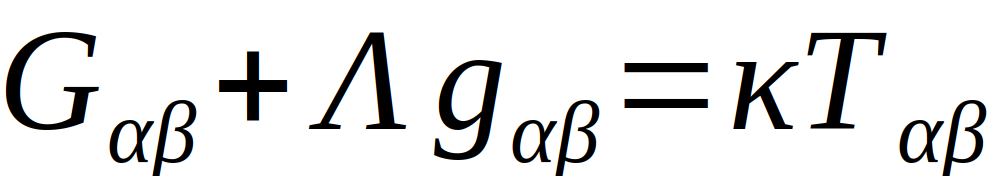
wobei G_αβ der Einstein-Tensor ist. Die kosmologische Konstante Λ war nicht Teil der ursprünglichen Formulierung der Feldgleichungen sondern wurde 1917 von Einstein hinzugefügt, um einen statischen Kosmos beschreiben zu können. Κ beschreibt die Einsteinsche Gravitationskonstante und lässt sich über

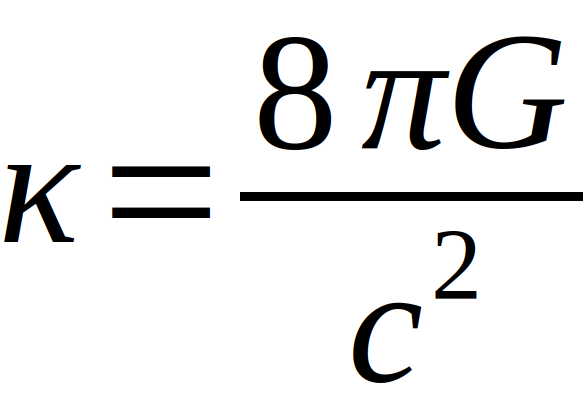
mit der Newtonschen Gravitationskonstante in Relation setzen, wobei c die Vakuum-Lichtgeschwindigkeit ist [1], [2], [3].

Die Feldgleichungen bilden ein System von zehn nichtlinearen, gekoppelten, partiellen Differentialgleichungen zur Bestimmung der Komponenten des Gravitationspotentials g_αβ.

Aus den Einstein-Gleichungen lässt sich die lokale Energie-Impuls-Erhaltungsgleichung herleiten, woraus sich wiederum die sogenannte geodätische Gleichung, also die Bewegungsgleichung der Allgemeinen Relativitätstheorie herleiten lässt:

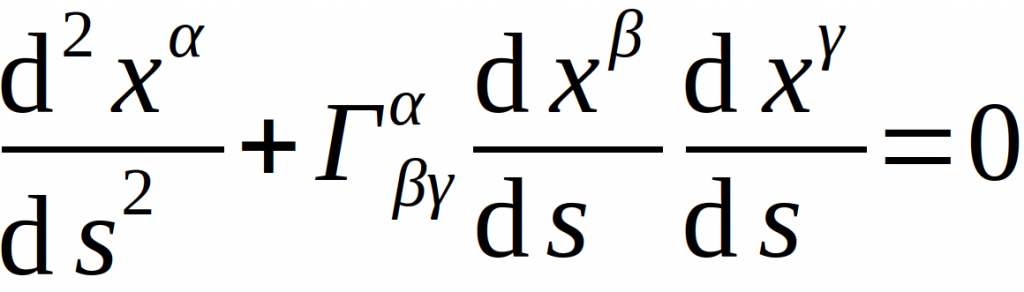
Die Einstein-Gleichung beschreibt wie sich die Materie im Universum der Raumzeit-Geometrie krümmen „soll“ und die Bewegungsgleichung beschreibt über die Raumzeit-Geometrie, wie sich die Materie bewegen „soll“. Letzteres zeigt den Einfluss des Machschen Prinzip in die Allgemeinen Relativitätstheorie [1], [3], [4].

[1] Lexikon der Physik: Allgemeine Relativitätstheorie, (Link: https://www.spektrum.de/lexikon/physik/allgemeine-relativitaetstheorie/383), aufgerufen am 29.07.2020

[2] Einstein, A.: Die Grundlage der allgemeinen Relativitätstheorie; Ann. D. Phys. 49; 1916

[3] Einstein, Albert: Über die spezielle und die allgemeine Relativitätstheorie; 2009

[4] D’Inverno, R.: Einführung in die Relativitätstheorie, 1995

Weiterführende Literatur:

[5] Ciufolini, I.; Wheeler, J.A.: Gravitation and Inertia, 1995

[6] Sexy, R.U.; Urbantke, H.K.: Gravitation und Kosmologie, 1995

[7] Mielke, E.W.: Sonne, Mond und … Schwarze Löcher, 1997

[8] Fließbach, Torsten: Allgemeine Relativitätstheorie, 2016

[9] Lämmerzahl, Claus: Am Rande des Messbaren. Quantengravitation im Experiment, 29.04.2008

[10] Boblest, Sebastian; Müller, Thomas; Wunner, Günther: Spezielle und allgemeine Relativitätstheorie, Grundlagen, Anwendungen in Astrophysik und Kosmologie sowie relativistische Visualisierung; 2016

Die Allgemeine Relativitätstheorie wurde 1915 von Albert Einstein aufgestellt, damals ohne empirische Grundlage.

In den folgenden Jahren wurden mehrere Experimente durchgeführt um die verschiedenen Vorhersagen der ART zu bestätigen. Generell können die Experimente in klassische und moderne aufgeteilt werden. Eines der klassischen Experimente handelt von der Periheldrehung des Planeten Merkur. Schon Ende des neunzehnten Jahrhunderts fiel Astronomen eine Diskrepenz von 43“ Bogensekunden in einhundert Jahren zwischen den Messungen der Geschwindigkeit der Periheldrehung und den Vorhersagen der damals verwendeten Newton‘schen Theorie auf. 1916, also erst einige Jahre später, konnte Einstein mit seiner kurz zuvor aufgestellten Allgemeinen Relativitätstheorie die Abweichung exakt berechnen und somit erklären. Wiederum drei Jahre später kam der öffentliche Durchbruch für die Theorie, als der Astronom Arthur Eddington 1919 den experimentellen Nachweis erbrachte, dass das Licht eines Sternes durch das Gravitationsfeld der Sonne abgelenkt wird und somit der Raum nach Einsteins Theorie gekrümmt ist [6]. Auch nach Newtons Theorie konnte eine Krümmung des Raumes berechnet werden, allerdings kam diese zu einem anderen Ergebnis (etwa halb so groß) als die ART. Das Experiment von Eddington fand während einer Sonnenfinsternis statt, da nur dann Sternenlicht gleichzeitig mit der verdunkelten Sonne beobachtet werden kann. Der Aufbau ist in der folgenden Abbildung dargestellt. Das Licht eines Sternes, das nahe an der Sonne vorbeiläuft und abgelenkt wird trifft dann auf die Erde und kann (scheinbar) beobachtet werden. Eigentlich könnte man den Stern nicht sehen, da sich seine wahre Position vom Beobachter aus hinter der Sonne befindet. Die wahre Position des Sterns kann jedoch berechnet werden und ergibt sich mit Hilfe der ART zu 1,75 Bogensekunden. Im Rahmen von Eddingtons Experiment konnte dieses Ergebnis der ART mit einer Unsicherheit von 20 % bestätigt werden. Seit der ersten Messung 1919 wurde das Experiment schon vielfach mit einer höheren Genauigkeit wiederholt und bestätigt [1] [2] [3].

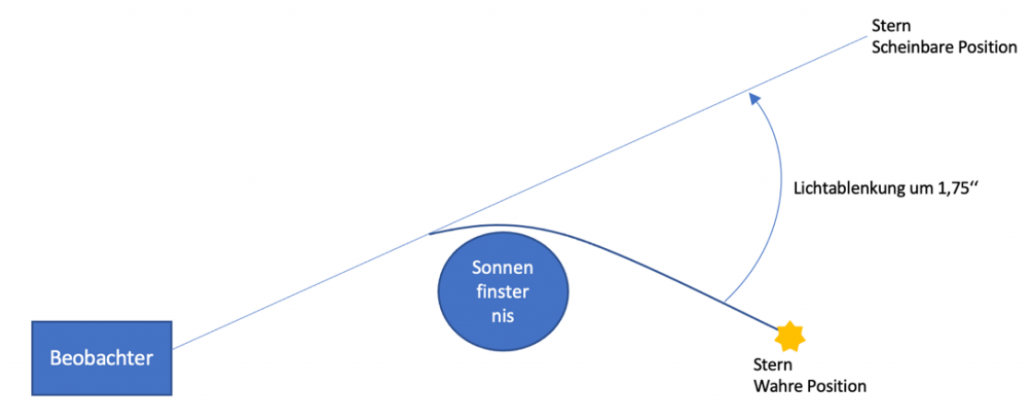
Ein weiteres Ergebnis der Allgemeinen Relativitätstheorie war die gravitative Rotverschiebung, also die Änderung der Lichtfrequenz ins Rote (sie wird geringer), wenn sich Licht von einem größeren zum kleineren Gravitationspotenzial bewegt. Auch diese Frequenzänderung lässt sich mit der ART berechnen. In einem Experiment der Physiker Pound und Rebka konnte 1960 die beschriebene Frequenzänderung nachgewiesen werden [7]. Der Aufbau befand sich in einem Turm, wobei am Boden (dem Erdpotential) eine Lichtquelle mit Gammastrahlung stand und ca. 22,6 m senkrecht nach oben zur Turmspitze (Turmpotential) strahlte. Vereinfacht kann die Änderung der Frequenz über

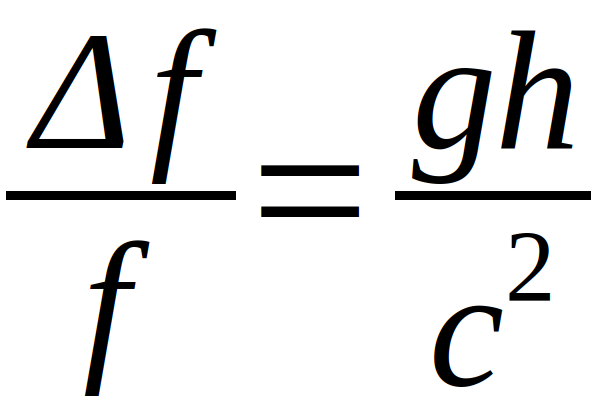
Mit g als Erdbeschleunigung, h als Höhe des Turmes und c als Lichtgeschwindigkeit berechnet werden. Die in dem Experiment gemessene Unsicherheit ergab sich mit der theoretischen Vorhersage von

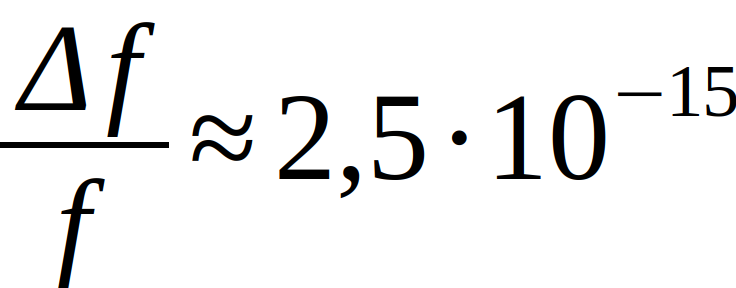
zu ca. 1 %. Der sogenannte Mößbauer-Effekt machte es möglich, diese kleine Abweichung der Frequenzen zu messen. Anzumerken ist weiter, dass auch durch die Ausdehnung des Raums eine Rotverschiebung hervorgerufen wird [1] [4].

Ein weiteres Experiment führe Shapiro 1968 und 1971 durch: eine Radar-Laufzeitmessung. Venus, Sonne und Erde liegen auf einer geraden Linie mit den Abständen r₁ von der Erde zur Sonne und dem Abstand r₂ von Venus zur Sonne, wobei die Venus, von der Erde aus gesehen, hinter der Sonne liegt [9] [10] [11].

Ein Radarsignal wird nun von der Erde bis zur Venus geschickt, dort reflektiert und dann auf der Erde wieder registriert. Die Vorhersage der ART lautet, dass auch die Laufzeit von Licht verändert wird, wenn es in die Nähe einer großen Masse kommt. Nach Newton lässt sich die Laufzeit wie folgt berechnen

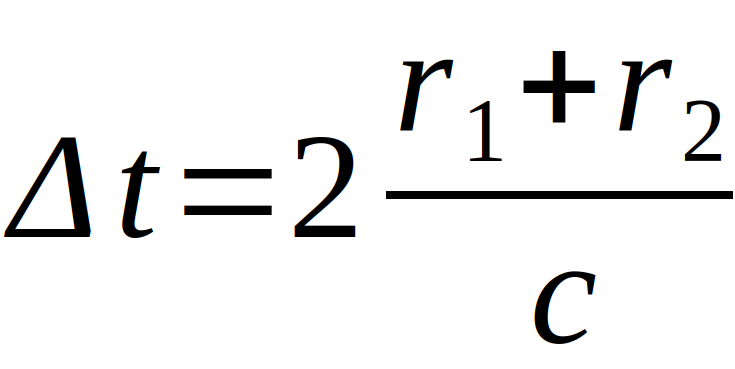
Nach Einstein ergibt sich numerisch eine Abweichung von und als Formelausdruck bzw. Korrekturterm (vereinfacht) zu

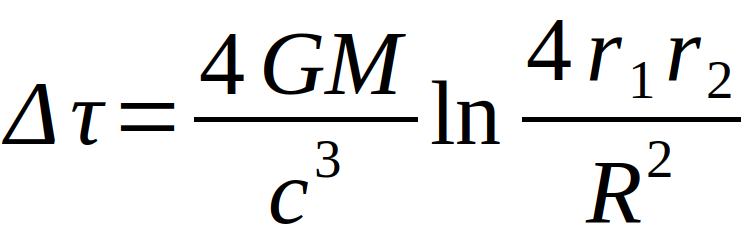
Wobei G die Newtonsche Gravitationskonstante, M die Masse der Sonne, R der Radius der Sonne und c die Lichtgeschwindigkeit ist. In Shapiros Experimenten konnte die berechnete Abweichung sehr gut experimentell nachgewiesen werden [1].

1971 führten Hafele und Keating ein Experiment durch, in dem die Zeitdifferenz einer Uhr auf der Erde mit der einer Flugzeuguhr verglichen wurde [12]. Bei einer äquatorialen Flugbahn ergibt sich laut der Allgemeinen Relativitätstheorie

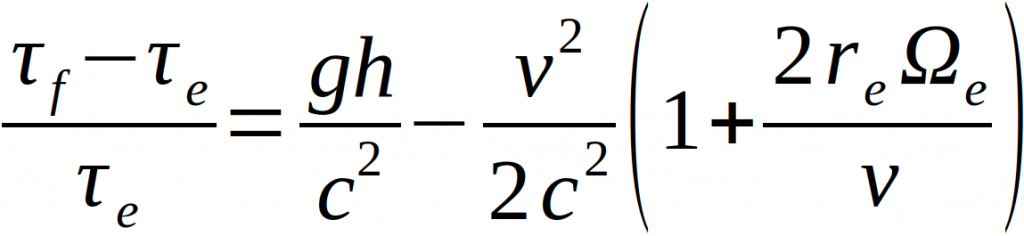
Mit τ_f und τ_e als Eigenzeiten für den Flugumlauf im Flugzeug bzw. auf der Erde, g als Erdbeschleunigung, h als Höhe des Flugzeugs, r_e als Erdradius, Ω_e als Drehgeschwindigkeit der Erde und c als Lichtgeschwindigkeit. Der erste Term stammt aus der ART und berücksichtigt die Gravitation, der zweite Term stammt aus der Speziellen Relativitätstheorie. Theoretisch ergibt sich somit

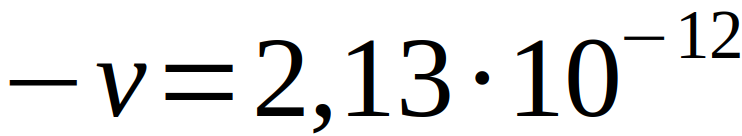
und

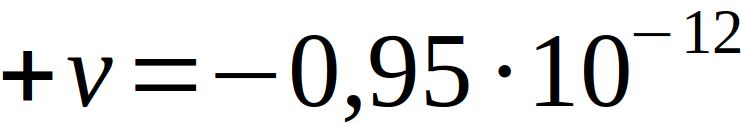
was sich mit den eingesetzten Atomuhren messen ließ.

Ein weiteres, bekanntes Experiment ist das Gravity Probe B Experiment, womit der Geodätische Effekt und der Lense Thirring Effekt nachgewiesen werden konnte.

Außerdem enthalten die Gleichungen der ART die sogenannten Gravitationswellen, die sich, wie elektromagnetische Wellen auch, mit Lichtgeschwindigkeit ausbreiten und immer dann entstehen, wenn Massen, z.B. bei der Bewegung von Planeten, beschleunigt werden. Die Intensität der Wellen ist sehr gering und sie werden durch viele äußere Störungen beeinflusst, was einen Nachweis sehr schwierig macht. In den 1960er Jahren versuchte der Physiker Joseph Weber die Ausdehnung eines Aluminiumzylinders, die durch Gravitationswellen zustande kam, zu messen, jedoch erfolglos [8] [13].

[1] Sonne, Bernd: Allgemeine Relativitätstheorie für jedermann: Grundlagen, Experimente und Anwendungen verständlich formuliert; Springer Spektrum; 2. Auflage; 2018

[2] Welt der Physik: Albert Einstein und die Relativitätstheorie; (Link: https://www.weltderphysik.de/thema/albert-einstein-und-die-relativitaetstheorie/), aufgerufen am 19.11.2020

[3] Fließbach, Thorsten: Allgemeine Relativitätstheorie; Springer Spektrum; 7. Auflage; 2016

[4] Göbel, Holger: Gravitation und Relativität: eine Einführung in die Allgemeine Relativitätstheorie; De Gruyter Studium; 2014

[5] Einstein, Albert: Die Grundlage der allgemeinen Relativitätstheorie; 1923

[6] Eddington, Sir Arthur: Space, Time and Gravitation – An Outline of the General Relativity Theory; Cambridge University Press; 1920

[7] Pound, R. V.; Rebka, G. A. Jr.: Gravitational Red-Shift in Nuclear Resonance; The Physical Review Journals Celebrate The International Year of Light; Phys. Rev. Lett. 3, 439; 01.11.1959

[8] Weber, J.: Gravitational Radiation; Phys. Rev. Lett. 18, 498; 27.03.1967

[9] Ash, M. E.; Campbell, D. B.; Dyce, R. B.; Ingalls, R. P.; Jurgens, R.; Pettengill, G. H.; Shapiro, I. I.: The Case for the Radar Radius of Venus; Science Vol 160, Issue 3831, 31.05.1968

[10] Shapiro, Irwin I.: Radar Observations of the Planets; Scientific American Vol. 219, No. 1; 07/1968

[11] Shapiro, Irwin I.; Ash, Michael E.; Ingalls, Richard P.; Smith, William B.; Campbell, Donald B.; Dyce, Raymond F. Jurgens; Pettengill, Gordon H.: Fourth Test of General Relativity: New Radar Result; Phys. Rev. Lett. 26; 1132; 03.05.1971

[12] Hafele, J. C.; Keating, Richard E.: Around-the-World Atomic Clocks: Predicted Relativistic Time Gains; Science Vol 177, Issue 4044; 14.07.1972

[13] Everitt, C. W. F. et al.: Gravity Probe B: Final Results of a Space Experiment to Test General Relativity; Phys. Rev. Lett. 106, 221101; 31.05.2011

Weiterführende Literatur:

[14] Eddington, Sir Arthur: Report on the relativity theory of gravitation; Minkowski Institute Press; 2014

[15] Horst, Wegener: Der Mössbauer-Effekt und seine Anwendungen in Physik und Chemie; Bibliographisches Institut, Mannheim; 1965

[16] Shapiro, Irwin I.; Pettengill, Gordon H.; Ash, Michael E.; Stone, Melvin L.; Smith, William B.; Ingalls, Richard P.; Brockelman, Richard A.: Fourth Test of General Relativity: Preliminary Results; Phys. Rev. Lett. 20, 1265; 27.05.1968, Erratum Phys. Rev. Lett. 21, 266; 1968

[17] Shapiro, Irwin I.: Planetary radar astronomy; IEEE Spectrum Volume 5, Issue 3; 05/1968

[18] Rodrigues Jr., W. A.; de Oliveira, E. C.: A comment on the twin paradox and the Hafele-Keating experiment; Physics Letters A; Volume 140, Issue 9; 16.10.1989

[19] Schlegel, Richard: Comments on the Hafele-Keating Experiment; American Journal of Physics 42, 183; 1974

[20] Everitt, C. W. F.; Mulfelder, B.; DeBra, D. B.; Parkinson, B. W.; Turneaure, J. P.; Silbergleit, A. S.; Acworth, E. B.; Adams, M.; Adler, R.; Bencze, W. J.: The Gravity Probe B test of general relativity; Classical and Quantum Gravity, Volume 32, Number 22; 17.11.2015

[21] Buchman, Saps; Everitt, C. W. F.; Perkinson, B.; et. Al.: The Gravity Probe B Relativity Mission; Advances in Space Research; Volume 25, Issue 6, 2000

[22] Conklin, John W.; Gravity Probe B Collaboration: The Gravity Probe B experiment and early results; Journal of Physics: Conference Series, Volume 140, Issue 1; 2008

Schwarze Löcher sind extrem massereiche Himmelsobjekte, so massereich, dass selbst Licht nicht mehr entweichen kann – sie lassen sich somit niemals direkt beobachten. Vorhergesagt wurden sie erstmals im Jahr 1939 von J. R. Oppenheimer und H. Snyder [1].

Laut der Definition der Allgemeinen Relativitätstheorie ist ein Schwarzes Loch eine spezielle Raumzeit, deren Krümmung von außen nach innen zunimmt und im Zentrum unendlich groß, also singulär, wird. Sie gelten als singuläre Lösung der Einsteinschen Feldgleichungen der Allgemeinen Relativitätstheorie. Da auch Licht in einer gekrümmten Raumzeit gekrümmten Bahnen folgt, bewegt es sich in dem singulären Bereich in unendlicher Krümmung und kommt somit nicht mehr aus diesem heraus, wodurch die Schwarzen Löcher als „schwarz“ gelten. Eine weitere Eigenschaft Schwarzer Löcher ist, dass keinerlei Information über Vorgänge im Inneren nach außen übermittelt wird, da das Gravitationspotential an der Oberfläche der Masse M so groß ist, dass die Frequenz der emittierten Strahlung (gravitationsbedingt) auf null rotverschoben wird. Die Frequenz wird null, sobald der Radius der Masse, der sogenannte Schwarzschildradius, in diesem Fall des schwarzen Lochs, den kritischen Wert erreicht [2], [3], [4].

In den vergangenen Jahren wurden zahlreiche schwarze Löcher gefunden und identifiziert, eins davon im Zentrum der Milchstraße in der Nähe der Radioquelle Sagittarius A*. Dieses schwarze Loch hat eine Masse von rund drei Millionen Sonnenmassen, wobei eine Sonnenmasse 1,99 * 10³⁰ kg entspricht. Ein schwarzes Loch mit einer Sonnenmasse hätte, falls so eines existierte, einen Durchmesser von ungefähr 3 km. Das uns am nächsten liegende Schwarze Loch befindet sich im Röntgendoppelstern XTE J1118+480 im Sternbild Ursa Major (Großer Bär) und hat eine Entfernung von 5870 Lichtjahren. Es wiegt etwa acht Sonnenmassen [3], [4].

Es existieren zum einen rotierende und zum anderen nicht rotierende Schwarze Löcher. Allen ist gemein, dass sie sowohl Teilchen als auch Strahlung (vermutlich) unwiederbringlich „verschlucken“ – sie wachsen durch die Massen und Drehimpulse der einfallenden Objekte. Geschehen kann das, sobald diese Objekte nah genug an den sogenannten Ereignishorizont, also den äußeren Rand, herankommen. Dieser Horizont ist keine feste Oberfläche, sondern eine mathematisch definierte Grenzfläche, an der die Entweichgeschwindigkeit gleich der Vakuumgeschwindigkeit wird [2].

Klassifiziert werden schwarze Löcher außerdem anhand einer Massenskala, da so die Unterscheidung der verschiedenen Typen mit ihrem jeweiligen Entstehungsmechanismus und ihren durchlaufenden Entwicklungen möglich ist. So werden sie aufgeteilt in Schwarze Mini-Löcher, Primordiale Schwarze Löcher, Stellare Schwarze Löcher, Mittelschwere Schwarze Löcher, Supermassereiche und massereiche oder superschwere Schwarze Löcher mit Massen von der, eines Elementarteilchens bis 10¹⁰ Sonnenmassen [2].

Im Laufe der Jahre wurden verschiedene Methoden zur Entdeckung Schwarzer Löcher entwickelt. Generell ist diese Entdeckung nur aufgrund ihrer Auswirkungen auf die Umgebung möglich. Methoden sind unter anderem die kinematische Verifikation, die eruptive Verifikation, die akkretive Verifikation, die spektro-relativistische Verifikation und die obskurative Verifikation [2].

[1] Oppenheimer, J. R.; Snyder, H.: On Continued Gravitational Contraction; Phys. Rev. 56, 455; 11.09.1939

[2] Lexikon der Astronomie: Schwarzes Loch; (Link: https://www.spektrum.de/lexikon/astronomie/schwarzes-loch/429), aufgerufen am 22.06.2020

[3] Stöcker et. At: Taschenbuch der Physik, 2018, Europa Lehrmittel Verlag

[4] Tipler, Llewellyn: Moderne Physik, 2010, Oldenbourg Verlag

Weiterführende Literatur:

[5] Hawking, A. W.: Gravitational Radiation in an Expanding Universe; Journal of Mathematical Physics 9, 598; 1968

[6] Hawking, S. W.: Gravitational Radiation from Colliding Black Holes; Phys. Rev. Lett. 26, 1344; 24.05.1971

[7] Robinson, Sean P.; Wilczek, Frank: Relationship between Hawking Radiation and Gravitational Anomalies; Phys. Rev. Lett. 95, 011303; 30.06.2005

[8] Zhang, Jingyi; Zhao, Zheng: Hawking radiation of charged particles via tunneling from the Reissner-Nordström black hole; Journal of High Energy Physics, Volume 2005; 19.10.2005

[9] Page, Don N.: Hawking radiation and black hole thermodynamics; New Journal of Physics, Volume 7; 29.09.2005

[10] Giddings, Steven B.: The black hole information paradox; 28.08.1995

[11] Hawking, S. W.: The Information Paradox for Black Holes; Talk given on 28.08.2015 at Hawking Radiation, conference held at KTH Royal Institute of Technology, Stockholm

[12] Mathur, Samir D.: A Proposal to resolve the black hole information paradox; International Journal of Modern Physics D, Vol 11, No. 10, 2002

Die Kosmologische Konstante Λ wurde im Jahr 1917 von Albert Einstein als neue Größe der sogenannten Kosmologie, der Lehre von der Entstehung und Entwicklung des Weltalls, eingeführt. In den Einsteinschen Feldgleichungen im Rahmen der Allgemeinen Relativitätstheorie, einem komplizierten Satz gekoppelter, partieller Differentialgleichungen, tauchte in Folge dessen der sogenannte Λ-Term auf. Während Einstein die Kosmologische Konstante angeblich als seine dümmste Eselei bezeichnete, gilt sie heute als eine zeitlich unveränderliche Form Dunkler Energie [1] [2].

Die Motivation Einsteins für die Einführung der Konstante rührte ursprünglich aus der Ästhetik, denn sein Ziel war es, ein statisches, homogenes Universum in eine konsistente Theorie einzubetten. Das damals favorisierte Weltmodell war ein eben solches, statisches Universum, ein dynamisches Universum, als welches wir es heute erachten, kam damals niemandem in den Sinn. Die Einsteinschen Feldgleichungen lassen sich auch ohne die kosmologische Konstante beschreiben, jedoch bedeutet das Weglassen der Konstante bzw. des Terms automatisch, dass das materieerfüllte Universum bzw. dessen Entwicklung nicht statisch sein kann und somit notwendigerweise expandieren oder kollabieren muss. Damit das Universum aufgrund der gravitativen Anziehung nicht kollabiert, führte Einstein damals die Konstante ein. Sofern sie positiv ist, beschreibt sie eine Art „Expansions-Kraft“, welche der gravitativen Anziehung entgegenwirkt. Das Problem mit der statischen Lösung war die Instabilität – kleinste Abweichungen von der idealen Materieverteilung ließen das Universum demnach je nach Vorzeichen der Störung expandieren oder kollabieren. Nachdem von Edwin Hubble anhand der Galaxienflucht die Expansion des Universums gezeigt werden konnte und Physiker wie Alexander Alexandrowitsch Friedmann und Georges Lemaître kosmologische expandierende Lösungen Einsteins Feldgleichungen entdeckten, verwarf dieser seine Idee der kosmologischen Konstante und betitelte sie als „größte Eselei meines Lebens“, da er die Konstante ursprünglich nur einführte, um die Expansion des Universums zu unterbinden und ein statisches Universum zu erhalten. In den 1990er Jahren wurde entdeckt, dass die beobachtete, stetige Galaxienflucht und Expansion des Universums nur für die ersten paar Milliarden Jahre seit dem Urknall gilt und dass die Expansionsgeschwindigkeit seit circa fünf Milliarden Jahren nicht mehr stetig ist, sondern beschleunigt. Damit konnte der Λ-Term in den Gleichungen der Allgemeinen Relativitätstheorie nicht weggelassen werden, sondern ist in angepasster Form in der heutigen Physik für die beschleunigte Ausdehnung des Universums verantwortlich [1], [3], [4], [5], [6].

Lange war die vorherrschende Meinung in der Physik, dass der Wert der kosmologischen Konstante null sei -neue Beobachtungen kommen jedoch zu einem sehr kleinen, aber positiven Wert. Mittlerweile gilt die Konstante als zeitlich konstante Energiedichte des Vakuums ρ_vac [kg m^-3]. Sie ergibt sich zu

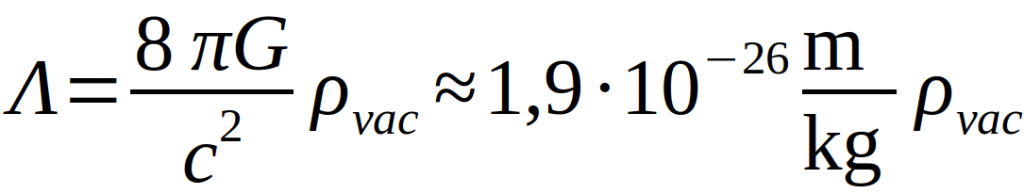
mit der Gravitationskonstante G, der Lichtgeschwindigkeit im Vakuum c und der Kreiszahl π. Ein positives Lambda bedeutet eine „kosmische Abstoßung“ (Antigravitation) und ein negatives Lambda „kosmische Anziehung“ [1], [4], [7].

[1] Spektrum: Lexikon der Astronomie: Kosmologische Konstante, (Link: https://www.spektrum.de/lexikon/astronomie/kosmologische-konstante/241), aufgerufen am 08.05.2020

[2] Einstein, Albert: Die Grundlage der allgemeinen Relativitätstheorie; Annalen der Physik, Vierte Folge, Band 49

[3] Konitzer, Franziska: Welt der Physik: Kosmologische Konstante, (Link: https://www.weltderphysik.de/mediathek/podcast/kosmologische-konstante/), aufgerufen am 08.05.2020

[4] Physik Cosmos-Indirekt: Kosmologische Konstante, (Link: https://physik.cosmos-indirekt.de/Physik-Schule/Kosmologische_Konstante), aufgerufen am 08.05.2020

[5] Osterbrock, Donald E.; Gwinn, Joel A.; Brashear, Ronald S.: Edwin Hubble and the Expanding Universe; Scientific American Vol. 269, No. 1; 07/1993

[6] Friedmann, Aleksandr (Translated by Brian Doyle): 125. On the Curvature of Space; Zeitschrift für Physik 10, 1922

[7] Krauss, Lawrence M.; Turner, Michael S.: The cosmological constant is back; General Relativity and Gravitation 27; 11/1995

Weiterführende Literatur:

[8] Vilsmeier, Dominik: Einsteins kosmologische Konstante: Unsinn oder eine neue Kraft?

[9] Zlatev, Ivaylo; Wang, Limin; Steinhardt, Paul J.: Quintessence, Cosmic Coincidence, and the Cosmological Constant; Phys. Rev. Lett. 82, 896; 01.02.1999

[10] Hiscock, William A.: Quantum instabilities and the cosmological constant; Volume 166, Issue 3; 16.01.1986

[11] Hawking, S. W.: The cosmological constant is probably zero; Physics Letters B, Volume 134, Issue 6; 26.01.1984

[12] Ostiker, J. P.; Steinhardt, Paul J.: The observational case for a low-density Universe with a non-zero cosmological constant; Nature 377; 19.10.1995

[13] Friedmann, Alexander A.: The Man Who Made The Universe Expand; American Journal of Physics 62, 1054; 1994

Supraleiter leiten bei Kühlung auf eine sehr geringe Temperatur (unter -139 °C) ohne Widerstand elektrischen Strom, d.h. ohne Energie zu verlieren. Diese Eigenschaft tritt aufgrund der Bildung sogenannter Cooper-Paare auf. In diesem Zustand können Elektronen durch das Material des Supraleiters, ohne auf Widerstand bzw. Hindernisse zu treffen, fließen. Bei Hochtemperatursupraleitern ergibt sich die Supraleitfähigkeit anders als bei den konventionellen nicht durch die Elektron-Photon-Wechselwirkung und es handelt sich nicht um metallische, sondern um keramische Materialien [1], [2]. Die Bezeichnung der Hochtemperatursupraleiter kommt daher, dass deutlich höhere Sprungtemperaturen erreicht werden können (Bis zu -23 °C).

Die Geschichte der Supraleiterforschung begann schon im Jahr 1911, als Heike Kamerlingh Onnes es als erster schaffte, Quecksilber mit Hilfe von flüssigem Helium auf circa vier Kelvin bzw. minus 269 °C herunter zu kühlen und somit Metalle in einem zuvor noch unbekanntem Temperaturbereich erforschen konnte. Damals waren die Vorstellungen darüber, wie ein elektrischer Leitmechanismus generell funktionieren könnte, noch sehr vage und lückenhaft [3], [4], [5].

Onnes Messinstrumente zeigten während seiner Experimente an, dass unterhalb der Temperatur von vier Kelvin das Metall (Quecksilber) den angelegten elektrischen Strom verlustfrei leitete, der elektrische Widerstand verschwand. 1913 konnte nachgewiesen werden, dass auch Blei unterhalb einer Temperatur von -266 °C zum Supraleiter wird und der elektrische Widerstand verschwindet. In den folgenden Jahren konnten immer weitere Materialien gefunden werden, die sich entsprechend verhalten. Die Temperatur, ab der das jeweilige Material zum Supraleiter wird, wird Sprungtemperatur genannt [3], [4], [5].

Die Idee, Supraleiter für technische Anwendungen zu nutzen, gab es schon 1913. Seither waren Physiker auf der Suche nach anderen Materialien mit einer höheren Sprungtemperatur, vor allem um die Anwendung praktikabler zu machen. Der (bis jetzt) bekannte Supraleiter mit der höchsten Sprungtemperatur ist das Quecksilber Kuprat mit einer Temperatur von 134 Kelvin (minus 139 °C, unter hohem Druck liegt die Sprungtemperatur bei 153 K bzw. minus 120 °C) und gilt somit als sogenannter Hochtemperatursupraleiter. Der Vorteil dieser Form der Supraleiter ist, dass dank der höheren Sprungtemperatur flüssiger Stickstoff statt flüssigem Helium verwendet werden kann, was den gesamten Prozess schon deutlich wirtschaftlicher macht. Das Problem mit den sogenannten Kupraten ist, dass sie sich sehr spröde verhalten und somit nur schwer verarbeitbar sind. Es gibt außerdem Forschung im Bereich der Materialmischungen aus z.B. Eisen, Lanthan, Phosphor, Sauerstoff und Arsen, allerdings konnten damit bis heute nur Sprungtemperaturen von 56 K bzw minus 217 °C erreicht werden [4].

Bleibt die Frage, warum sich Supraleiter so verhalten, wie sie es tun. Grundsätzlich funktioniert die Supraleitung aufgrund des Auftretens einer makroskopischen, kohärenten Materialwelle, durch die Elektronenpaare, die sogenannten Cooper-Paare, gebildet werden. Aufgestellt wurde diese erfolgreiche Theorie 1957 von John Bardeen, Leon Cooper und Robert Schrieffer und ist unter dem Namen BCS-Theorie bekannt. Sie besagt, dass Elektronen in einem Supraleiter aufgrund von Wechselwirkungen zwischen Elektronen und dem Kristallgitter bei niedrigen Temperaturen zu Paaren gekoppelt sind. Das Verhalten Hochtemperatursupraleiter wird durch die Theorie nur teilweise beschrieben [6], [7].

Eine der neuesten Entdeckungen war 2018 die, dass auch hauchdünne Schichten aus Kohlenstoff supraleitende Eigenschaften zeigen. Werden zwei Graphenschichten übereinandergelegt und um einen Winkel von 1,3 Grad gegeneinander verdreht, zeigen sich bei Herunterkühlen auf eine Temperatur von -271,5 °C supraleitende Eigenschaften. Die Hoffnung ist nun, das Verhalten der sogenannten unkonventionellen Supraleiter (Hochtemperatursupraleiter) mit den verdrehten Graphenschichten genauer untersuchen zu können [8], [9].

[1] Spektrum: Supraleiter, (Link: https://www.spektrum.de/thema/supraleiter/1314677), aufgerufen am 06.05.2020

[2] Welt der Physik: Supraleiter, (Link: https://www.weltderphysik.de/gebiet/materie/supraleiter/), aufgerufen am 06.05.2020

[3] Buckel, Werner; Kleiner, Reinhold: Supraleitung – Grundlagen und Anwendungen; WILEY-VCH; 2004

[4] Pollmann, Maike: Welt der Physik: Geschichte der Supraleitung, (Link: https://www.weltderphysik.de/gebiet/materie/supraleiter/geschichte/), 07.04.2011; aufgerufen am 07.05.2020

[5] Onnes, Heike Kamerlingh; Edited by Gavroglu, Kostas; Goudaroulis, Yorgos: Through Measurement to Knowledge: The Selected Papers of Heike Kamerlingh Onnes 1853- 1926; Boston Studies in the Philosophy of Science Volume 124; 1991

[6] Tipler, Paul; Llewellyn, Ralph: Moderne Physik; Oldenbourg; 2010

[7] Cooper, Leon N.; Feldman, Dmitri: BCS: 50 Years; World Scientific Publishing CO. Ptc. Ltd.; 2011

[8] Löfken, Jan Oliver: Welt der Physik: Supraleiter aus Kohlenstoff, (Link: https://www.weltderphysik.de/gebiet/materie/news/2018/supraleiter-aus-kohlenstoff/), 05.03.2018, aufgerufen am 07.05.2020

[9] Cao, Yuan; Fatemi, Valla; Fang, Shiang; et. Al.: Unconventional superconductivity in magic-angle graphene superlattices; Nature 556; 05.03.2018

Weiterführende Literatur:

[10] Kempf, Achim: Could the Casimir Effect explain the Energetics of High-Temperature Superconductors?; arXiv 03/2006

[11] Kiehn, R. M.: Are There Three Kinds Of Superconductivity?; International Journal of Modern Physics B, 06/1991

[12] Rao, C. N. R.; Raychaudhuri, A. K.: CRC Handbook of chemistry and physics, CRC Press, 2004

[13] Donglu, Shi: High-Temperature Superconducting Materials Science and Engineering: New Concepts and Technology, Pergamon Press, 1995

[14] Mankowsky, Roman: Supraleitung bei Raumtemperatur; Physik in unserer Zeit Colume 46, 09/2015

Der Casimir-Effekt wurde erstmals von dem Physiker Hendrik Brugt Gerhard Casimir im Jahre 1948 berechnet und vorhergesagt. Der experimentelle Nachweis folgte 1956. Der Effekt besagt, dass sich zwei parallele Metallplatten (bzw. leitfähige Platten) im Vakuum anziehen, beziehungsweise eine Kraft, die Casimir-Kraft, wirkt, die die Platten zusammendrückt [1] [2] [3] [4] [5].

Um den Casimir-Effekt zu erklären, sollte erst einmal geklärt werden, aus was ein Vakuum besteht. Ein Vakuum ist ein Quantenfeld, also eine Überlagerung aus verschiedenen Feldkonfigurationen mit großen und kleinen Wellenlängen. Die Quantenfeldtheorie besagt, dass jedes Vakuum Energie, die sogenannte Nullpunktsenergie oder Vakuumenergie, enthält, welche allerdings nicht entzogen werden kann, da das Vakuum bereits den Zustand der niedrigsten Energie beschreibt. Hinter diesem „Nichts“ des Quantenvakuums befindet sich jedoch ein sehr komplexes Gebilde, wodurch es unmöglich ist, einen Raum von allen Teilchen zu entleeren. Die Partikel in diesem scheinbar leeren Raum existieren immer nur kurzzeitig, es existieren also Fluktuationen im Quantenvakuum [2], [3].

Der Casimir-Effekt basiert auf der Tatsache, dass ein elektrisches Feld auf parallelen Metallplatten nur senkrecht stehen kann. Dadurch werden die Möglichkeiten, wie sich diese Felder in dem Bereich zwischen den Platten ausbilden können, stark eingeschränkt und Konfigurationen mit Wellenlängen größer als der Plattenabstand sind nicht mehr möglich. Das Vakuum befindet sich in diesem Bereich in einem anderen Zustand als im „ungestörten“ Vakuum. Durch dieses Einschränken der Möglichkeiten sinkt dort die Nullpunktsenergie. Schiebt man die Platten nun noch näher zusammen verstärkt sich dieser Effekt weiter, die Platten ziehen sich an und eine kleine, aber messbare Energie wird gewonnen [1], [2].

Der Casimir-Effekt hat besonders in den letzten Jahren wieder mehr an Bedeutung und Aktualität gewonnen, da moderne Messtechniken wie zum Beispiel atomare Kraftmikroskopie dazu geführt haben, immer kleinere Kräfte mit deutlich höherer Genauigkeit messen zu können. Auch aus technologischer Sicht erhöhte sich das Interesse, da die Casimir-Kraft besonders bei Miniaturmaschinen im Mikro- und Nanometerbereich wichtig wird. In der Grundlagenforschung und besonders bezüglich des Bestrebens, die Gravitationstheorie, die Relativitätstheorie und die Quantenmechanik zu vereinigen spielt die Casimir-Kraft ebenfalls eine wichtige Rolle, besonders wenn es darum geht die von Physikern vorausgesetzten fundamentalen Kräfte experimentell nachzuweisen. Da diese Kräfte das Newtonsche Gravitationsgesetzt für Distanzen im Submillimeterbereich ändern, muss hier die Casimir-Kraft berücksichtigt vorausgesagt und berechnet werden können [6].

[1] Spektrum: Lexikon der Astronomie: Casimir-Effekt; (Link: https://www.spektrum.de/lexikon/astronomie/casimir-effekt/61), aufgerufen am 14.05.2020

[2] Physik Cosmos indirekt; (Link: https://physik.cosmos-indirekt.de/Physik-Schule/Casimir-Effekt), aufgerufen am 14.05.2020

[3] Spektrum: Lexikon der Astronomie: Quantenvakuum; (Link: https://www.spektrum.de/lexikon/astronomie/quantenvakuum/376), aufgerufen am 18.05.2020

[4] Plunien, Günter; Müller, Berndt; Greiner, Walter: The Casimir effect; Physics Reports Volume 134; 03/1986

[5] Casimir, H. B. G.: Mathematics. – On the attraction between two perfectly conducting plates; Gems from a century of science 1898-1997; 29.05.1948

[6] Lambrecht, Astrid: Das Vakuum kommt zu Kräften; Physik Unserer Zeit, 2005

Weiterführende Literatur:

[7] Milton, Kimball A.: The Casimir Effect: Physical Manifestations of Zero-Point Energy; University of Oklahhoma, 02/2008

[8] Antonini, P.; Bimonte, G.; et. Al.: An experimental apparatus for measuring the Casimir effect at large distances; 12/2008

[9] Quach, James Q.: Gravitational Casimir effect, 02/2015

[10] Mostepanenko, V. M.: Experiment, theory and the Casimir effect, 03/2009

[11] Bachmann, Sven; Kempf, Achim: The Transplanckian Question and the Casimir Effect, 04/2005

[12] Bordag, M.; Mohideen, U.; Mostepanenko, V. M.: New developments in the Casimir effect; Physics Reports Volume 353; 10/2001