Das Äquivalenzprinzip, auch Einstein‘sches Äquivalenzprinzip genannt, gilt als die der Allgemeinen Relativitätstheorie zugrunde liegende Hypothese. Sie sagt aus, dass ein homogenes Gravitationsfeld einem gleichmäßig beschleunigten Bezugssystem äquivalent ist. Anders ausgedrückt bedeutet das, dass die schwere und die träge Masse eines Körpers zwei äquivalente Größen sind [1] [2] [3] [4].
Anschaulich betrachtet kann ein Beobachter in einem abgeschlossenen System (Kasten) nicht unterscheiden, ob sich dieser Kasten auf der Oberfläche einer Masse und somit in dessen Gravitationsfeld befindet oder ob er gleichmäßig durch eine konstant wirkende Kraft ohne Gravitationsfeld im freien Raum beschleunigt wird. Einstein erkannte 1907 dieses Grundprinzip einer Theorie der Gravitation, welches ihn schließlich zur Allgemeinen Relativitätstheorie führte [5] [6].
Es existieren zwei Formen: das schwache und das starke Äquivalenzprinzip. Das schwache Äquivalenzprinzip sagt aus, dass von allen Eigenschaften eines Körpers die Masse (=Maß der Trägheit) bestimmt, welche Schwerkraft in einem gegebenen homogenen Gravitationsfeld auf ihn wirkt, wodurch Eigenschaften wie die Größe, Form oder chemische Zusammensetzung keinerlei Einfluss darauf haben [7].
Beim starken Äquivalenzprinzip gilt, dass Gravitations- und Trägheitskräfte auf kleinen Abstands- und Zeitskalen in einem Sinn äquivalent sind, indem sie an ihren Wirkungen nicht unterschieden werden können, weder mechanisch noch durch andere Beobachtungen [7].
Es gilt, dass die Massen in der Form
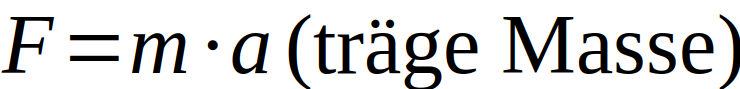
und
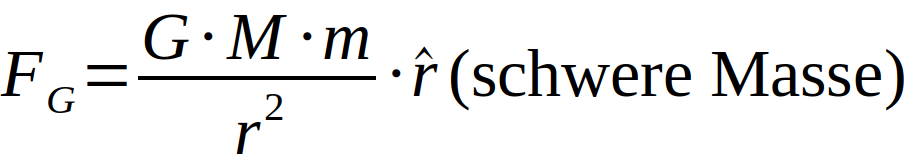
identisch sind [2].
Aus dem starken Äquivalenzprinzip folgt das schwache – ob diese Beziehung auch umgekehrt gilt ist Gegenstand aktueller Forschung und noch nicht geklärt.
Das schwache Prinzip konnte bereits durch diverse Experimente mit relativer Genauigkeit von bis zu 10-13 bestätigt werden, sodass
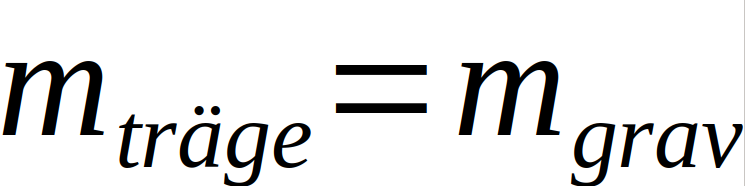
mit dieser Genauigkeit gilt. Die Folgerung des Prinzips ist also, dass es keine absolute Beschleunigung gibt und geben kann, sie ist, wie die Geschwindigkeit auch, immer relativ [2].
Der Physiker Eötvös führte bereits Ende des 19. Jahrhunderts Experimente mit einer Torsionswaage durch. Er wollte überprüfen, ob Körper aus unterschiedlichen Materialien in voneinander abweichende Richtungen fallen und somit das Verhältnis von schwerer und träger Masse bei den Messobjekten überprüfen. Solche Messungen zur Äquivalenz werden quantitativ über den sogenannten Eötvös-Faktor η beschrieben [8]:
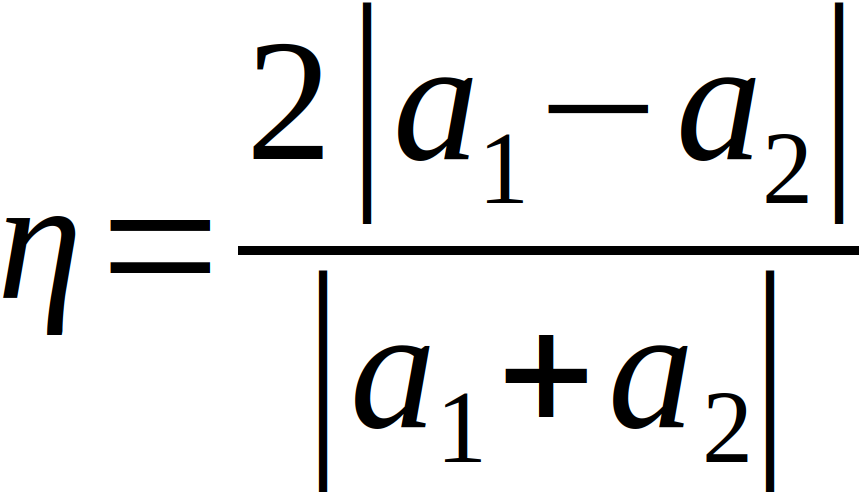
Mit a1 und a2 als gemessene Beschleunigungen der unterschiedlichen Testkörper [7] [9].
Die Torsionspendelversuche von Eötvös konnten die Grenze η auf weniger als 10-9 begrenzen. Mittlerweile hat die Eöt-Wash Gruppe der University of Washington in Seattle den Parameter η mit einer Materialkombination aus Beryllium und Titan im Gravitationsfeld der Erde bis auf eine Genauigkeit von 10-13 begrenzen können, das heißt, bis auf diese verbliebene Messungenauigkeit gilt dieser Teil des Äquivalenzprinzips [9] [10].
Schärfere Obergrenzen von η können beispielsweise durch satellitengestützte Experimente erreicht werden. In Frage kommen z.B. die STEP-Mission, Gravity Probe A oder auch MICROSCOPE [11] [12]. Die Idee dieser Experimente ist die Messung der relativen Beschleunigungen von im Orbit befindlichen, frei fallenden Testkörpern unterschiedlicher chemischer Zusammensetzung. Die zu erwartende Genauigkeit beträgt weniger als 10-15 bei MICROSCOPE und sogar < 10-18 bei STEP [7].
[1] Lexikon der Physik: Äquivalenzprinzip, (Link: https://www.spektrum.de/lexikon/physik/aequivalenzprinzip/712), aufgerufen am 29.06.2020 [2] Tipler, Paul; Llewellyn, Ralph: Moderne Physik, Oldenbourg Verlag [3] Pössel, Markus: Kabine, Schwerkraft und Rakete: Das Äquivalenzprinzip; Einstein online (Link: https://www.einstein-online.info/spotlight/aequivalenzprinzip/), aufgerufen am 14.08.2020 [4] Hagedorn, Daniel; Selig, Hanns: MICROSCOPE: Äquivalenzprinzip im Weltraumtest, (Link: https://www.weltderphysik.de/gebiet/universum/teleskope-und-satelliten/microscope/), aufgerufen am 18.08.2020 [5] Lexikon der Astronomie: Äquivalenzprinzip, (Link: https://www.spektrum.de/lexikon/astronomie/aequivalenzprinzip/21), aufgerufen am 29.06.2020 [6] Einstein, Albert: Die Grundlage der allgemeinen Relativitätstheorie; Annalen der Physik, Vierte Folge, Band 49 [7] Äquivalenzprinzip (Physik), Physik Cosmos, (Link: https://physik.cosmos-indirekt.de/Physik-Schule/%C3%84quivalenzprinzip_(Physik)), aufgerufen am 29.06.2020 [8] Eötvös, Roland: Über die Anziehung der Erde auf verschiedene Substanzen; Akadémiai Értesíto, 02/1890 [9] Guilini, Domenico: Einstein im Quantentest, Spektrum der Wissenschaft 10/13 – Oktober 2013 [10] The Eöt-Wash Group: Laboratory Tests of Gravitational and Sub-Gravitational Physics; (Link: https://www.npl.washington.edu/eotwash), aufgerufen am 18.08.2020 [11] Space Microscope to test universality of freefall, The European Space Agency, 2016; (Link: http://m.esa.int/Our_Activities/Space_Science/Space_Microscope_to_test_universality_of_freefall), aufgerufen am 18.08.2020 [12] Bergé, Joel; Rodrigues, Manuel; Touboul, Pierre: Status of MICROSCOPE, a mission to the test the Equivalence Principle in SpaceWeiterführende Literatur:
[13] Han, Feng-Tian; Wu, Qui-Ping; Zhou, Ze-Bing; et. Al.: Proposed Space Test of the New Equivalence Principle with Rotating Extended Bodies [14] Wagner, T. A.; Schlamminger, S.; Gundlach, J. H.; Adelberger, E. G.: Torsion-balance tests of the weak equivalence principle [15] Eötvös, Roland; Pekár Desiderius; Fekete, Eugen: Beiträge zum Gesetze der Proportionalität von Trägheit und Gravität [16] Fischbach, Ephraim: Reanalysis of the Eötvös Experiment