Die Gravitationskonstante G stammt aus dem Newtonschen Gravitationsgesetz und beschreibt die Anziehungskraft zweier Körper der Massen m1 und m2 im Schwerpunktsabstand r über die Formel
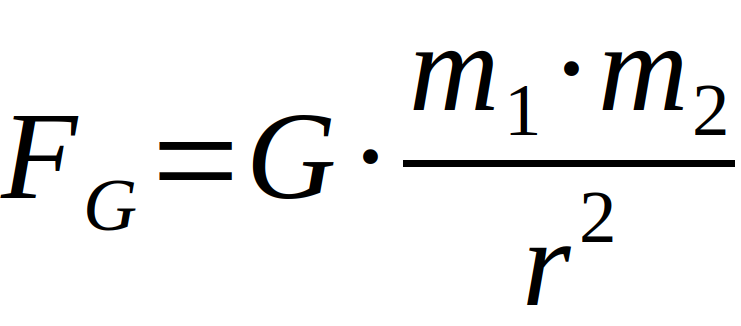
Da sie die schwächste der bekannten Wechselwirkungen ist und sich nicht abschirmen lässt, ist sie die mit der geringsten Genauigkeit gemessene Naturkonstante [1], [2], [3].
Im Jahr 1798 wurde die Gravitationskonstante erstmals von Cavendish bestimmt [2], [4]. Seither wurden mehr als 300 Versuche vorgenommen, doch selbst jüngste Messungen weisen Abweichungen von bis zu 0,055 % auf. Besonders für die Quantengravitation würden genauere Ergebnisse der Messungen neue Möglichkeiten eröffnen.
1998 wurden anlässlich einer „Zweihundertjahrfeier“ der ersten Messung der Gravitationskonstante die Ergebnisse der G-Messungen von 12 Forscherteams mit jeweils sehr unterschiedlichen Apparaturen verglichen. Die Genauigkeit ist in der folgenden Tabelle in ppm angegeben [5], [6].
| Labor | G * 1011 | (ppm) |
|---|---|---|
| New Zealand MSL | 6,6742(6) | 90 |
| Zürich | 6,6749(14) | 210 |
| Wuppertal | 6,6735(9)(13) | 240 |
| JILA | 6,6873(94) | 1400 |
| BIPM | 6,683(11) | 1650 |
| Karagioz (Russia) | 6,6729(5) | 75 |
| Luther/ Towler | 6,6726(5) | 64 |
| PTB | 6,71540(56) | 83 |
Es ist zu erkennen, dass die verschiedenen Institute zwar mit einer Genauigkeit von 0,001 % gemessen haben, die Ergebnisse jedoch um bis zu 0,5 % voneinander abweichen.
Dieser Vergleich und die sich ergebenen Diskrepanzen resultierte im Jahr 2000 in einer Reihe neuer Messungen und neuer Experimente. Die Forscher Steve Merkowitz und Jens Gundlach entwickelten daraufhin einen Cavendish Apparat, mit dem sie die Ungenauigkeit um einen Faktor 10 senken konnten. Ihr Apparat folgte grundlegend dem Aufbau der Cavendish Torsionswaage, allerdings bauten sie einen zusätzlichen Rückkopplungsmechanismus ein, um die Testmassen zu bewegen, und somit die Verdrillung des Pendels auf ein Minimum zu beschränken [7], [8].
Nach ihren Ergebnissen liegt der Wert der Gravitationskonstante bei

mit einer Unsicherheit von 0,0014 % [2], [7]. Diese Messung ermöglichte, gemeinsam mit Daten des Lageos Satelliten, die bis dahin genaueste Bestimmung der Erd- und der Sonnenmassen [2], [3].
Aufgrund der vielen Messungen, die in den letzten 25 Jahren vorgenommen wurden und den Diskrepanzen, die die Ergebnisse mit sich brachten, legte das Committee on Data for Science and Technology (CODATA) 2014 den vorgeschlagenen Wert für die Gravitationskonstante auf
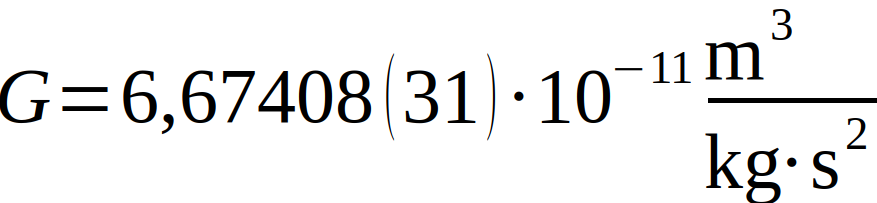
mit einer Unsicherheit von 0,0047 % [9].
Es ist nicht auszuschließen, dass die Abweichungen der Messungen ihren Ursprung in unentdeckten Eigenschaften der Gravitation haben, allerdings ist das eher unwahrscheinlich. Wahrscheinlicher ist es, dass bisher unentdeckte systematische Fehler eine genauere Bestimmung verhindern [3].
Im Rahmen von Messreihen an der Bergischen Universität Wuppertal wurden als primäre Fehlerquellen der Messungen der sogenannte Choke-Effekt (der Effekt, dass Variationen des Abstandes zwischen dem Spiegel und dem Drosselflansch zu Änderungen der Resonanzfrequenz führen), die Neigung des Stützgerüstes aufgrund der Deformation des Fundamentes durch die Testmassen sowie die Positionierung der Testmassen genannt [1].
2018 konnten chinesische Forscher durch Änderungen zweier Experimentaufbauten die Ungenauigkeit der Messungen erneut reduzieren. Beim Ersten Aufbau hing ein vergoldeter Quarzblock an einer Glasfaser und zwei 778 g schwere Stahlkugeln waren die Testmassen. Beim zweiten Versuch befanden sich Torsionspendel und Stahlkugeln auf je einem Drehtisch, damit sie unabhängig voneinander rotieren können und die Verdrillung des Fadens so unterbunden werden kann. Aus diesen beiden Versuchen ergaben sich zwei unterschiedliche Werte für die Gravitationskonstante, beide in dem der CODATA festgelegten Bereich. Die Unsicherheit von 0,0047 % konnte somit auf 0,0012 % gesenkt werden. Warum die beiden Werte der chinesischen Experimente trotzdem recht stark voneinander abweichen, ist immer noch unklar [10], [11].
[1] Kleinevoß, Ulf: Bestimmung der Newtonschen Gravitationskonstanten G; Bergische Universität Gesamthochschule Wuppertal [2] LEIFIphysik Joachim Herz Stiftung: Gravitationsgesetz und -feld: Ausblick Gravitationskonstante (Link: https://www.leifiphysik.de/mechanik/gravitationsgesetz-und-feld/ausblick/gravitationskonstante), aufgerufen am 25.06.2020 [3] Makro und Mikrokosmos: Berechnung der Gravitationskonstante G (Link: https://www.makro-und-mikrokosmos.de/berechnung-der-gravitationskonstante-g-aus-drei-naturkonstanten-der-quantenphysik/), aufgerufen am 25.06.2020 [4] Cavendish, Henry: XXI. Experiments to determine the Density of the Earth, 21.06.1798 [5] Kestenbaum, David: Gravity Measurements Close in on Big G, 18.12.1998 [6] Newman, Riley: Convergence (?) of G Measurements – Mysteries Remain, University of California, 03.2003 [7] Physics central: Big ‚G‘ (Link: https://www.physicscentral.com/explore/action/bigg.cfm), aufgerufen am 25.06.2020 [8] Gundlach, Jens H.; Merkowitz, Stephen M.: Measurement of Newton’s Constant Using a Torsion Balance with Angular Acceleration Reedbach, Phys. Rev. Lett. 85, 2869; 02.10.2000 [9] Mohr, Peter; Newell, David; Taylor, Barry: CODATA Recommended Values of the Fundamental Physical Constants: 2014 [10] Scharf, Rainer: Gravitationskonstante genauer denn je gemessen (Link: https://www.pro-physik.de/nachrichten/gravitationskonstante-genauer-denn-je-gemessen), aufgerufen am 25.06.2020 [11] Wu, Junfei; Li, Qing; Liu, Jianping; et. Al.: Progress in Precise Measurements of the Gravitatinal Constant, Annalen der Physik, Volume 531, 08.04.2019Weiterführende Literatur:
[12] Wolschin, G.: Schwierige Bestimmung einer fundamentalen Naturkonstante [13] Schlamminger, S.; Gundlach, J.H.; Newman, R.D.: Recent measurements of the gravitational constant as a function of time, Phys. Rev. D 91, 11.06.2015 [14] Newman, Riley D.: The Challenge of Measuring G, The Ninth Marcel Grossmann Meeting, 2002