Die Cavendish-Waage (auch Gravitationswaage genannt) beruht auf einem Experiment des Wissenschaftlers Henry Cavendish, welches im Jahr 1798 das erste Mal durchgeführt wurde. Cavendishs eigentliches Ziel war es, die Dichte der Erde bestimmen zu können – er interessierte sich selbst nicht für die Gravitationskonstante, es gelang durch sein Experiment trotz dessen, den Wert der von Isaac Newton in seinem Gravitationsgesetz beschriebene Gravitationskonstante G, annähernd genau zu errechnen [1], [2].
Im Wesentlichen handelt es sich bei der Cavendish-Waage um eine Drehwaage, die auf der auf einen Draht aufgebrachten Torsionskraft beruht, d.h. der Betrag des Winkels, um den dieser Draht ausgelenkt wird, gibt Auskunft über das wirkende Drehmoment und die zwischen den Testmassen wirkende Kraft lässt sich berechnen. Genauer bedeutet das, dass sich in der Mitte der Waage ein Draht befindet, an dessen Ende ein waagerechter Stab angebracht ist. An dessen Mitte ist ein Spiegel und an dessen Enden jeweils eine kleine Masse befestigt. Davor befindet sich eine Lichtquelle, welche einen möglichst konzentrierten Lichtstrahl emittiert, heutzutage z.B. ein Laser. Dieser Lichtstrahl ist auf den Torsionsdraht gerichtet und wird von dem Spiegel auf einen Schirm reflektiert. Sobald nun eine Auslenkung der Massen aus der Ruhelage geschieht, verschiebt sich der Lichtpunkt [1].
Um das Experiment durchzuführen, werden nun zwei große Massen M im gleichen Abstand r zu den kleineren Massen positioniert. Die Massen m und M auf den gegenüberliegenden Seiten ziehen sich an und der Stab mitsamt dem Spiegel wird sich leicht verdrehen – der Lichtpunkt wird sich auf dem Schirm um die Strecke s0 bewegen und das System gerät in eine gedämpfte Schwingung. Anschließend wird der Stab mit den schweren Massen um fast 180° gedreht, wodurch sich der Effekt umkehren wird und die Auslenkung in die entgegengesetzte Richtung auftritt.
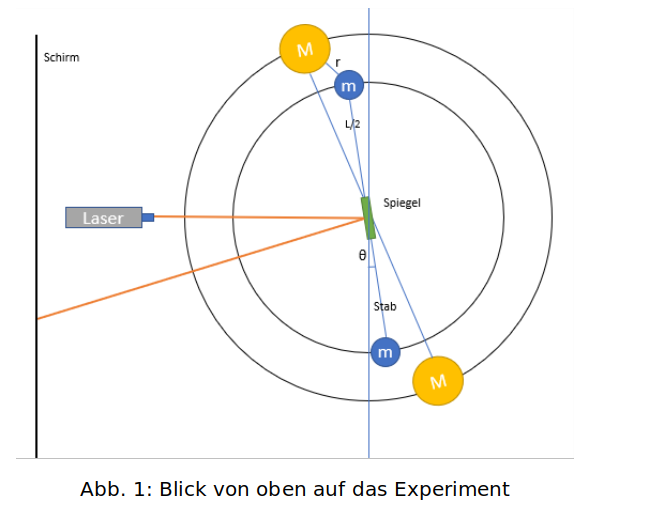
Um die Gravitationskonstante zu erhalten bzw. zu berechnen, müssen nun die Hebellänge des Stabes L, die Entfernung zum Schirm S sowie die Masse M bekannt sein. Unter der Annahme, dass die Abstände zwischen den kleinen und großen Massen klein gegenüber der gesamten Systemgröße sind, ergibt sich für das auftretende Drehmoment an der Stange
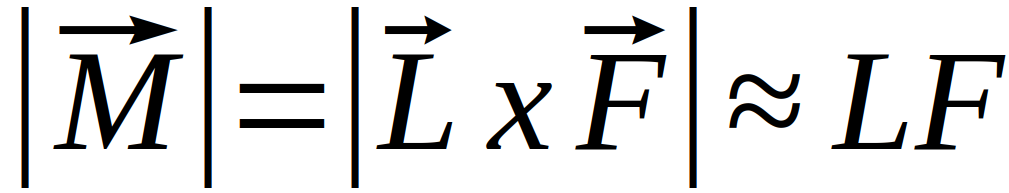
Durch die Anziehung der Massen mit kleinem Abstand r wird ein Drehmoment erzeugt, welches auf den Stab wirkt und sich nach folgender Formel ergibt
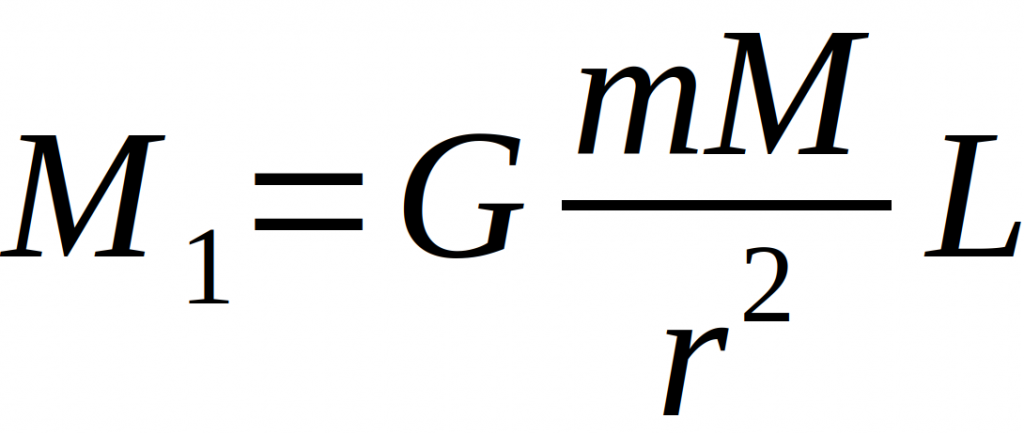
Auch die jeweils gegenüberliegende große Masse M bewirkt eine Kraft auf die jeweilige andere kleine Masse nach
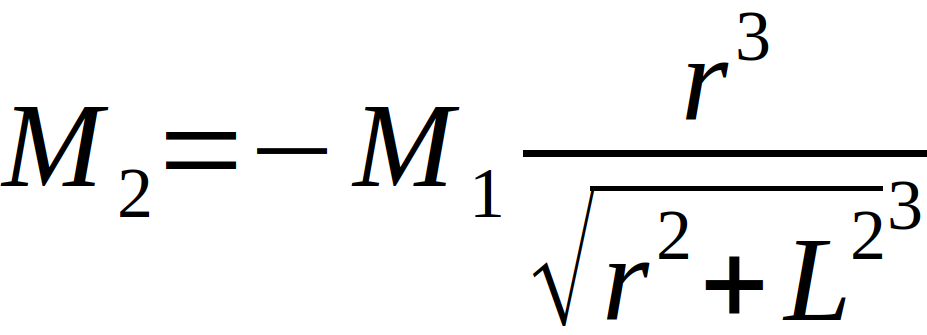
Das resultierende Drehmoment Mres ergibt sich aus der Summe von M1 und M2, die korrespondierende Gegenkraft ist die Festigkeit des Drahtes, welche sich aus dem Direktionsmoment D und dem Winkel Theta ergibt. Es gilt also
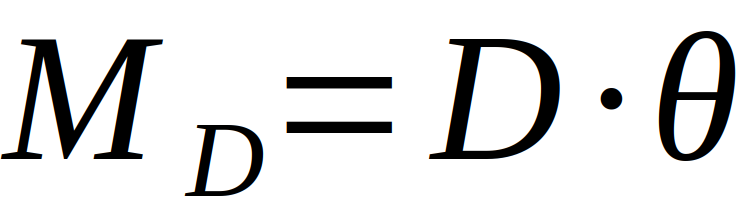
Beziehungsweise für das Kräftegleichgewicht
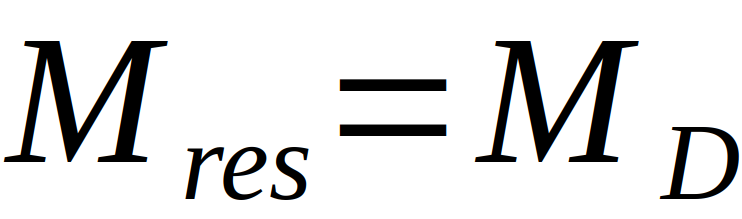
Dadurch, dass Drehschwingungen in der linearen Näherung harmonisch sind, ist die Kreisfrequenz Omega nur abhängig von dem Direktionsmoment D und dem Trägheitsmoment. Das Trägheitsmoment lässt sich direkt nach
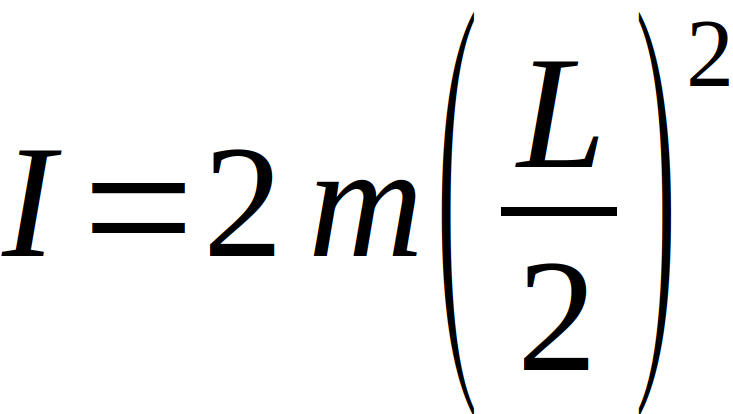
bestimmen. Mit diesem Wert sowie der Formel für die Schwingungsdauer
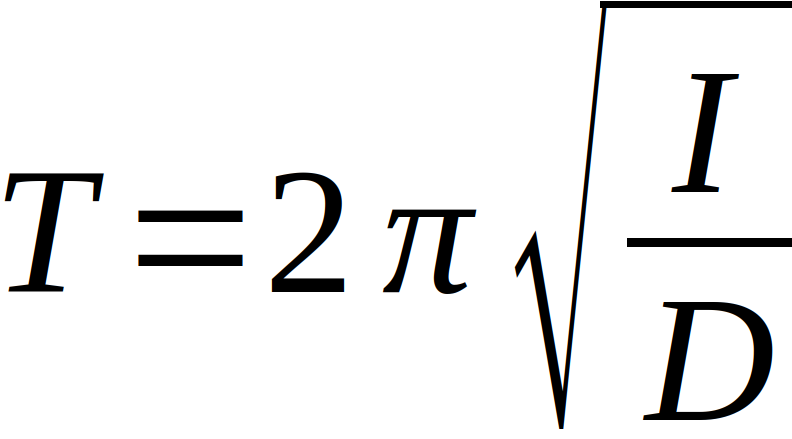
lässt sich direkt auf das gesuchte Direktionsmoment D schließen. Es ergibt sich
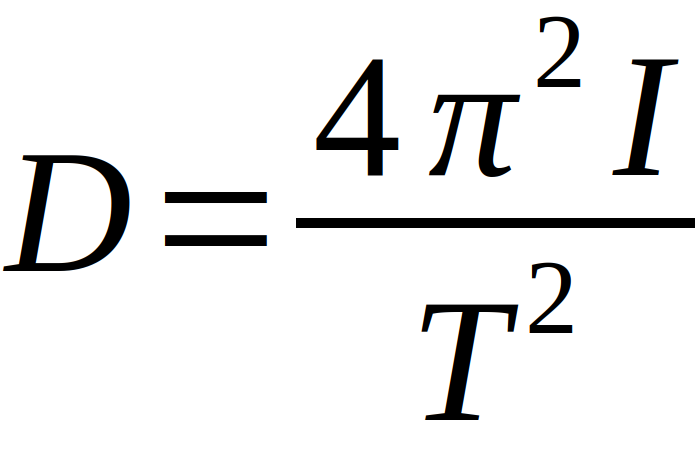
Der Drehwinkel Theta, welcher ebenfalls in die Gegenkraft MD eingeht, ergibt sich über die Auslenkung des Spiegels, denn es gilt generell bei allen Spiegeln: Der Drehwinkel der Abbildung ist doppelt so groß, wie der Drehwinkel des Spiegels selbst. Bei der Annahme eines leicht gewölbten Schirms ergibt sich für den Winkel
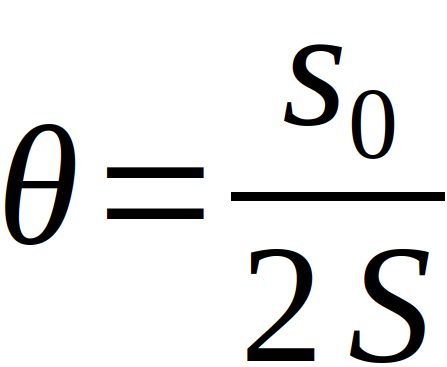
Setzt man diese Erkenntnisse nun in das Kräftegleichgewicht ein, kann nach der Gravitationskonstante umgeformt werden und es ergibt sich [1], [2]
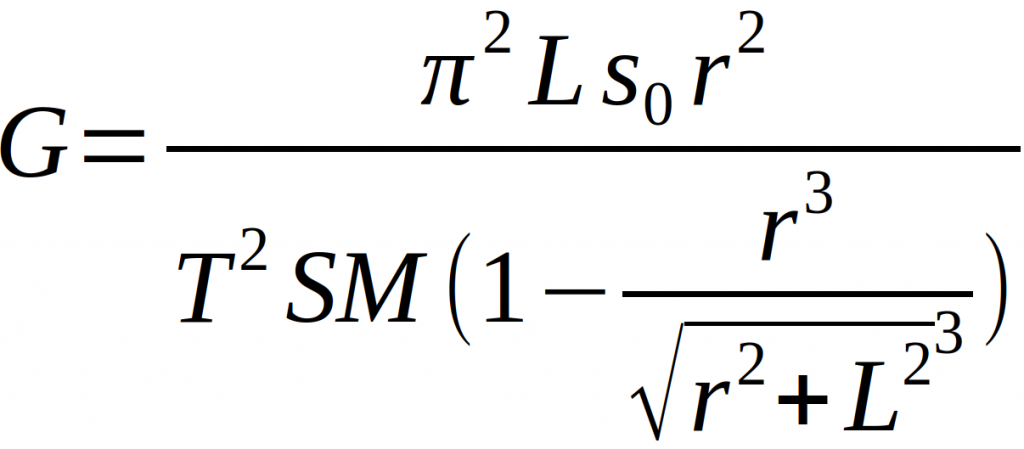
Henry Cavendish war es somit als erstem möglich, die Gravitationskonstante mit hoher Genauigkeit zu bestimmen. Sein Ergebnis lautete
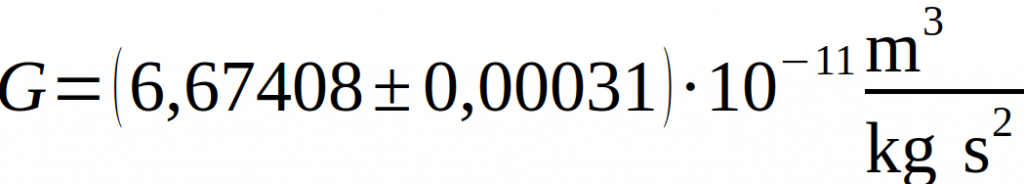
Durch die spezielle Konstruktion der Gravitationswaage können sehr kleine Kräfte gemessen werden, weshalb sie neben den beschriebenen Experimenten auch für weitere Entdeckungen genutzt wurde, wie z.B. die Bestimmung der Coulombkraft elektrisch geladener Körper.
[1] Physik Cosmos (Link: https://physik.cosmos-indirekt.de/Physik-Schule/Gravitationswaage), aufgerufen am 05.05.2020 [2] Cavendish, Henry: XXI. Experiments to determine the Density of the Earth; 21.06.1798; (Link: https://upload.wikimedia.org/wikipedia/commons/0/0b/Cavendish-Experiments_to_Determine_the_Density_of_the_Earth..pdf) [3] Rundel, Michael, et al.: Physik Libre, 2020Weiterführende Literatur:
[4] Panov, V. I.; Frontov, V. N.: The Cavendish experiment at large distances; 25.05.1979, Moscow State University [5] Al Balushi, Abdulrahim; Cong, Wan; Mann, Robert B.: Optomechanical quantum Cavendish; Phys. Rev. A 98, 043811, 05.10.2018 [6] Mostepanenko, V. M.; Sokoliv, I. Yu.: New restrictions on the parameters of the spin-1 antigravitation following from the Casimir effect, Eötvös and Cavendish experiments; Physics Letters A, Volume 132, 17.10.1988 [7] Clotfelter, B. E.: The Cavendish experiment as Cavendish knew it; American Journal of Physics 55; 04.06.1998 [8] Brill, Dieter: The Cavendish Experiment in General Relativity; In: Harvey A. (eds) On Einstein’s Path; Springer, New York, 1999